M1Q0c: Dimensional Analysis

Introduction

This section explores dimensional analysis. This section includes worked examples, sample problems, and a glossary.

Note to students:  The concepts covered in this section should be familiar to you from your previous high school science classes.  For some of you, this material will still be fresh in your mind, and this content will be useful reference as you complete the homework.  For other people, it may have been several years since you encountered this content, and you’ll need to read and study this section.

Learning Objectives for Dimensional Analysis:

  • Use dimensional analysis for unit conversions and relating different quantities.
    | Dimensional Analysis |

| Key Concepts and Summary | Glossary | End of Section Exercises |

Dimensional Analysis

It is often the case that a quantity of interest may not be easy (or even possible) to measure directly but instead must be calculated from other directly measured properties and appropriate mathematical relationships. For example, consider measuring the average speed of an athlete running sprints. This is typically accomplished by measuring the time required for the athlete to run from the starting line to the finish line, and the distance between these two lines, and then computing speed from the equation that relates these three properties:

speed = \dfrac{\text{distance}}{\text{time}}

An Olympic-quality sprinter can run 100 m in approximately 10 s, corresponding to an average speed of

\dfrac{\text{100 m}}{\text{10 s}} = 10 m/s

Note that this simple arithmetic involves dividing the numbers of each measured quantity to yield the number of the computed quantity (100/10  =  10) and likewise dividing the units of each measured quantity to yield the unit of the computed quantity (m/s  =  m/s). Now, consider using this same relation to predict the time required for a person running at this speed to travel a distance of 25 m. The same relation between the three properties is used, but in this case, the two quantities provided are a speed (10 m/s) and a distance (25 m). To yield the sought property, time, the equation must be rearranged appropriately:

time = \dfrac{\text{distance}}{\text{speed}}

The time can then be computed as:

\dfrac{\text{25 m}}{\text{10 m/s}} = 2.5 s

Again, arithmetic on the numbers (25/10 = 2.5) is accompanied by the same arithmetic on the units (\frac{\text{m}}{\text{m/s}} = s) to yield the number and unit of the result, 2.5 s. Note that, just as for numbers, when a unit is divided by an identical unit (in this case, m/m), the result is “1”—or, as commonly phrased, the units “cancel.”

These calculations are examples of a versatile mathematical approach known as dimensional analysis (or the factor-label method). Dimensional analysis is based on this premise: the units of quantities must be subjected to the same mathematical operations as their associated numbers. This method can be applied to computations ranging from simple unit conversions to more complex, multi-step calculations involving several different quantities.

Conversion Factors and Dimensional Analysis

A ratio of two equivalent quantities expressed with different measurement units can be used as a unit conversion factor. For example, the lengths of 2.54 cm and 1 in. are equivalent (by definition), and so a unit conversion factor may be derived from the ratio,

\dfrac{\text{2.54 cm}}{\text{1 in.}} (2.54 cm = 1 in.) or 2.54 \frac{\text{cm}}{\text{in}}

Several other commonly used conversion factors are given in Table 1, and more can be found in Appendix C.

Table 1. Common Conversion Factors
Length Volume Mass
1 m  =  1.0936 yd 1 L  =  1.0567 qt 1 kg  =  2.2046 lb
1 in.  =  2.54 cm (exact) 1 qt  =  0.94635 L 1 lb  =  453.59 g
1 km  =  0.62137 mi 1 ft3  =  28.317 L 1 (avoirdupois) oz  =  28.349 g
1 mi  =  1609.3 m 1 tbsp  =  14.787 mL 1 (troy) oz  =  31.103 g

When we multiply a quantity (such as distance given in inches) by an appropriate unit conversion factor, we convert the quantity to an equivalent value with different units (such as distance in centimeters). For example, a basketball player’s vertical jump of 34 inches can be converted to centimeters by:

34 in. × \dfrac{\text{2.54 cm}}{\text{1}\;\rule[0.5ex]{1em}{0.1ex}\hspace{-1em}\text{in.}} = 86 cm

Since this simple arithmetic involves quantities, the premise of dimensional analysis requires that we multiply both numbers and units. The numbers of these two quantities are multiplied to yield the number of the product quantity, 86, and the units are multiplied to yield \frac{\text{in.} \times \text{cm}}{\text{in.}}. Just as for numbers, a ratio of identical units is also numerically equal to one, \frac{\text{in.}}{\text{in.}}  =  1, and the unit product thus simplifies to cm. (When identical units divide to yield a factor of 1, they are said to “cancel.”) Using dimensional analysis, we can determine that a unit conversion factor has been set up correctly by checking to confirm that the original unit will cancel, and the result will contain the sought (converted) unit.

Example 1

Using a Unit Conversion Factor
The mass of a competition frisbee is 125 g. Convert its mass to ounces using the unit conversion factor derived from the relationship 1 oz = 28.349 g (Table 1).

Solution
If we have the conversion factor, we can determine the mass in kilograms using an equation similar the one used for converting length from inches to centimeters.

x oz = 125 g × unit conversion factor

We write the unit conversion factor in its two forms:

\dfrac{1\;\text{oz}}{28.349\;\text{g}} and \dfrac{28.349\;\text{g}}{1\;\text{oz}}

The correct unit conversion factor is the ratio that cancels the units of grams and leaves ounces.

x oz = 125 g × \dfrac{\text{1 oz}}{\text{28.349}\;\rule[0.25ex]{1em}{0.1ex}\hspace{-0.8em}\text{g}} = \dfrac{125}{28.349} oz = 4.41 oz (3 significant figures)

Check Your Learning
Convert a volume of 9.345 qt to liters.

Answer:

8.844 L

Beyond simple unit conversions, dimensional analysis can be used to solve more complex problems involving computations. Regardless of the details, the basic approach is the same—all the dimensional units involved in the calculation must be appropriately oriented to ensure that they appropriately cancel and/or combine to yield the desired unit in the result. This is why it is referred to as the dimensional analysis. As your study of chemistry continues, you will encounter many opportunities to apply this approach.

Example 2

Computing Quantities from Measurement Results and Known Mathematical Relations
What is the density of common antifreeze in units of g/mL? A 4.00 qt sample of the antifreeze weighs 9.26 lb.

Solution
Since density = \dfrac{\text{mass}}{\text{volume}}, we need to divide the mass in grams by the volume in milliliters. In general: the number of units of B = the number of units of A × unit conversion factor. The necessary conversion factors are given in Table 1: 1 lb = 453.59 g; 1 L = 1.0567 qt; 1 L = 1,000 mL. We can convert mass from pounds to grams in one step:

9.26 lb × \dfrac{453.59\;\text{g}}{1\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{lb}} = 4.20 × 103 g

We need to use two steps to convert volume from quarts to milliliters.

  1. Convert quarts to liters.
    4.00 qt × \dfrac{1\;\text{L}}{1.0567\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{qt}} = 3.78 L
  2. Convert liters to milliliters.
    3.78 L × \dfrac{1000 \;\text{mL}}{\rule[0.7ex]{1em}{0.1ex}\hspace{-0.8em}\text{L}} = 3.78 L × 103 mL

Then,

density = \dfrac{4.20 \times 10^3 \;\text{g}}{3.78 \times 10^3 \;\text{mL}} = 1.11 g/mL

Alternatively, the calculation could be set up in a way that uses three unit conversion factors sequentially as follows:

\dfrac{9.26\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{lb}}{4.00\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{qt}} × \dfrac{453.59\;\text{g}}{1\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{lb}} × \dfrac{1.0567\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{qt}}{1\;\rule[0.7ex]{1em}{0.1ex}\hspace{-0.8em}\text{L}} × \dfrac{1\;\rule[0.7ex]{1em}{0.1ex}\hspace{-0.8em}\text{L}}{1000\;\text{mL}} = 1.11 g/mL

Check Your Learning
What is the volume in liters of 1.000 oz, given that 1 L = 1.0567 qt and 1 qt = 32 oz (exactly)?

Answer:

2.957 × 10-2 L

Example 3

Computing Quantities from Measurement Results and Known Mathematical Relations
While being driven from Philadelphia to Atlanta, a distance of about 1250 km, a 2014 Lamborghini Aventador Roadster uses 213 L gasoline.

  1. What (average) fuel economy, in miles per gallon, did the Roadster get during this trip?
  2. If gasoline costs $3.80 per gallon, what was the fuel cost for this trip?

Solution
(a) We first convert distance from kilometers to miles:

1250 km × \dfrac{0.62137\;\text{mi}}{1\;\rule[0.5ex]{1.5em}{0.1ex}\hspace{-1.5em}\text{km}} = 777 mi

and then convert volume from liters to gallons:

213 L × \dfrac{1.0567\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{qt}}{1\;\rule[0.7ex]{1em}{0.1ex}\hspace{-0.8em}\text{L}} × \dfrac{1\;\text{gal}}{4\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{qt}} = 56.3 gal

Then,

(average) mileage = \dfrac{777 \;\text{mi}}{56.3\;\text{gal}} = 13.8 miles/gallon = 13.8 mpg

Alternatively, the calculation could be set up in a way that uses all the conversion factors sequentially, as follows:

\dfrac{1250\;\rule[0.5ex]{1.5em}{0.1ex}\hspace{-1.5em}\text{km}}{213\;\rule[0.7ex]{1em}{0.1ex}\hspace{-0.8em}\text{L}} × \dfrac{0.62137\;\text{mi}}{1\;\rule[0.5ex]{1.5em}{0.1ex}\hspace{-1.5em}\text{km}} × \dfrac{1\;\rule[0.7ex]{1em}{0.1ex}\hspace{-0.8em}\text{L}}{1.0567\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{qt}} × \dfrac{4\;\rule[0.5ex]{1.1em}{0.1ex}\hspace{-1em}\text{qt}}{1\;\text{gal}} = 13.8 mpg

(b) Using the previously calculated volume in gallons, we find:

56.3 gal × \dfrac{\$3.80}{1\;\rule[0.5ex]{1.5em}{0.1ex}\hspace{-1.4em}\text{gal}} = $214

Check Your Learning
A Toyota Prius Hybrid uses 59.7 L gasoline to drive from San Francisco to Seattle, a distance of 1300 km (two significant digits).

  1. What (average) fuel economy, in miles per gallon, did the Prius get during this trip?
  2. If gasoline costs $3.90 per gallon, what was the fuel cost for this trip?

Answer:

(a) 51 mpg; (b) $62

Key Concepts and Summary

It is often useful or necessary to convert a measured quantity from one unit into another. These conversions are accomplished using unit conversion factors, which are derived by applications of a mathematical approach called dimensional analysis. This strategy is also employed to calculate sought quantities using measured quantities and appropriate mathematical relations.

Glossary

dimensional analysis
versatile mathematical approach that can be applied to computations ranging from simple unit conversions to more complex, multi-step calculations involving several different quantities
unit conversion factor
ratio of equivalent quantities expressed with different units; used to convert from one unit to a different unit

Chemistry End of Section Exercises

  1. The label on a soft drink bottle gives the volume in two units: 2.0 L and 67.6 fl oz. Use this information to derive a conversion factor between the English and metric units. How many significant figures can you justify in your conversion factor?
  2. A barrel of oil is 42 gallons. How many liters of oil are in a barrel? (1 liter = 1.05669 quarts; 4 quarts = 1 gallon)
  3. Convert 5.94 cubic centimeters to cubic meters.

Answers to Chemistry End of Section Exercises

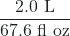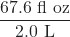  1. The conversion factor can be presented two ways: \dfrac{\text{2.0 L}}{\text{67.6 fl oz}} or \dfrac{\text{67.6 fl oz}}{\text{2.0 L}}.  Only two significant figures are justified.
  2. 160 L
  3. 5.94 × 10-6 m3
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.