M6Q4: Heat Capacity
Introduction
This section explores the application of thermodynamics concepts to everyday life. We will introduce the concept of heat capacity and learn how this concept allows us to calculate the energy gain or loss of a substance by measuring its temperature change upon heating or cooling. This section includes worked examples, sample problems, and a glossary.
Learning Objectives for Heat Capacity
- Identify the relationship between heat, mass, temperature change, and heat capacities and solve problems that quantify heat flow.
| Heat Capacity |
| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |
Heat Capacity
Imagine a flame placed below a beaker of water. The water warms up and eventually starts to boil. Why? The flame is caused by the combustion of methane (natural gas), which is exothermic. The energy released by the combustion reaction causes molecules in air (mostly N2 and O2) to translate, rotate, and vibrate faster. These high kinetic energy molecules bang into the thin glass beaker, which is composed mostly of silicon and oxygen atoms. These Si and O atoms start to vibrate more because of collisions with the hot air. Next, the water molecules in contact with the beaker warm up because they are in contact with the high kinetic energy Si and O atoms. The water molecules then translate and rotate and vibrate faster too, and they transfer their energy to water molecules throughout the beaker. How much more energy do these water molecules have? Remember that temperature is a measure of the average kinetic energy per molecule. The more energy that is added to the water, the higher the average kinetic energy per molecule, and therefore the higher the temperature. The energy transfer is the form of heat, q, and the temperature change is ΔT. The ratio of these numbers is called the heat capacity, C:
C = ![]()
Think of heat capacity as a measure of the ability of molecules to store energy. Substances with a higher heat capacity have more ways to store energy (energy can be stored as vibrations, rotations, and even hydrogen bonds). Molecules act like little batteries, storing energy through their motions. The heat capacity can also be higher just because there is more substance to heat up—heat capacity is another extensive property. Therefore, C varies both with the identity and the amount of substance. We can easily measure the heat capacity and then covert it into a molar quantity, Cm, to provide the heat capacity per mole of substance. This gives us tremendous insight into the various ways that atoms and molecules move and store energy. For example, the molar heat capacity of iron is 25 J/(mol·K), just one-third the value for water of 75 J/(mol·K). Why might water have a molar heat capacity so much higher than iron?
Next, let’s looks at some examples and how heat capacity enters our daily lives. For example, consider the heat capacities of two cast iron frying pans. The heat capacity of the large pan is five times greater than that of the small pan because, although both are made of the same material, the mass of the large pan is five times greater than the mass of the small pan. More mass means more atoms are present in the larger pan, so it takes more energy to make all of those atoms vibrate faster. (Figure 1).

The heat capacity of the small cast iron frying pan is found by observing that it takes 18,150 J of energy to raise the temperature of the pan by 50.0 °C:
Csmall pan = ![]() = 363 J/°C
= 363 J/°C
The larger cast iron frying pan, while made of the same substance, requires 90,700 J of energy to raise its temperature by 50.0 °C. The larger pan has a (proportionally) larger heat capacity because the larger amount of material requires a (proportionally) larger amount of energy to yield the same temperature change:
Clarge pan = ![]() = 1814 J/°C
= 1814 J/°C
The specific heat capacity (c) of a substance, commonly called its “specific heat,” is the quantity of heat required to raise the temperature of 1 gram of a substance by 1 degree Celsius (or 1 kelvin):
c = ![]()
Specific heat capacity depends only on the kind of substance absorbing or releasing heat. It is an intensive property—the type, but not the amount, of the substance is all that matters. For example, the small cast iron frying pan has a mass of 808 g. The specific heat of iron (the material used to make the pan) is therefore:
ciron = ![]() = 0.449
= 0.449 ![]()
The large frying pan has a mass of 4040 g. Using the data for this pan, we can also calculate the specific heat of iron:
ciron = ![]() = 0.449
= 0.449 ![]()
Although the large pan is more massive than the small pan, since both are made of the same material, they both yield the same value for specific heat (for the material of construction, iron). Note that specific heat is measured in units of energy per temperature per mass and is an intensive property, being derived from a ratio of two extensive properties (heat and mass). The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and has units of J/(mol·°C).
Liquid water has a relatively high specific heat (about 4.184 J/(g·°C)); most metals have much lower specific heats (usually less than 1 J/(g·°C)). The specific heat of a substance varies somewhat with temperature. However, this variation is usually small enough that we will treat specific heat as constant over the range of temperatures that will be considered in this chapter. Specific heats of some common substances are listed in Table 1. This table is also reproduced in Appendix E for reference. Note that the units of specific heat J/(g·°C), are identical to J/(g·K) and no conversion is needed between the two. This is because the temperature component in the definition of specific heat is a change in temperature, and with 1 °C being exactly the same size as 1 K, it is the same whether expressed in °C or K.
| Substance | Symbol (state) | Specific Heat (J/(g·°C)) |
|---|---|---|
| helium | He(g) | 5.193 |
| water | H2O(ℓ) | 4.184 |
| ethanol | C2H6O(ℓ) | 2.376 |
| ice | H2O(s) | 2.093 (at −10 °C) |
| water vapor | H2O(g) | 1.864 |
| nitrogen | N2(g) | 1.040 |
| oxygen | O2(g) | 0.918 |
| aluminum | Al(s) | 0.897 |
| carbon dioxide | CO2(g) | 0.853 |
| argon | Ar(g) | 0.522 |
| iron | Fe(s) | 0.449 |
| copper | Cu(s) | 0.385 |
| lead | Pb(s) | 0.130 |
| gold | Au(s) | 0.129 |
| silicon | Si(s) | 0.712 |
If we know the mass of a substance and its specific heat, we can determine the amount of heat, q, entering or leaving the substance by measuring the temperature change before and after the heat is gained or lost:
q = (specific heat) × (mass of substance) × (temperature change)
q = c × m × ∆T = c × m × (Tfinal – Tinitial)
In this equation, c is the specific heat of the substance, m is its mass, and ΔT (which is read “delta T”) is the temperature change, Tfinal − Tinitial. If a substance gains thermal energy, its temperature increases (i.e., its final temperature is higher than its initial temperature and Tfinal − Tinitial has a positive value), and the value of q is positive. If a substance loses thermal energy, its temperature decreases (i.e., the final temperature is lower than the initial temperature and Tfinal − Tinitial has a negative value), and the value of q is negative.
Example 1
Measuring Heat
A flask containing 8.0 × 102 g of water is heated, and the temperature of the water increases from 21 °C to 85 °C. How much heat did the water absorb?
Solution
To answer this question, consider these factors:
- the specific heat of the substance being heated (in this case, water)
- the amount of substance being heated (in this case, 800 g)
- the magnitude of the temperature change (in this case, from 21 °C to 85 °C).
The specific heat of water is 4.184 J/(g·°C), so to heat 1 g of water by 1 °C requires 4.184 J. We note that since 4.184 J is required to heat 1 g of water by 1 °C, we will need 800 times as much to heat 800 g of water by 1 °C. Finally, we observe that since 4.184 J are required to heat 1 g of water by 1 °C, we will need 64 times as much to heat it by 64 °C (that is, from 21 °C to 85 °C).
This can be summarized using the equation:
q = c × m × ∆T = c × m × (Tfinal – Tinitial) = (4.184 ![]() ) × (800 g) × (85 °C – 21 °C)
) × (800 g) × (85 °C – 21 °C)
q = (4.184 ![]() ) × (800 g) × (64 °C) = 210,000 J = 210 kJ
) × (800 g) × (64 °C) = 210,000 J = 210 kJ
Because the temperature increased, the water absorbed heat and q is positive.
Check Your Learning
How much heat, in joules, must be added to a 5.00 × 102 g iron skillet to increase its temperature from 25 °C to 250 °C? The specific heat of iron is 0.449 J/(g·°C).
Answer:
5.05 × 104 J (50.5 kJ)
Note that the relationship between heat, specific heat, mass, and temperature change can be used to determine any of these quantities (not just heat) if the other three are known or can be deduced.
Example 2
Determining Other Quantities
A piece of unknown metal weighs 348 g. When the metal piece absorbs 6.64 kJ of heat, its temperature increases from 22.4 °C to 43.6 °C. Determine the specific heat of this metal (which might provide a clue to its identity).
Solution
Since mass, heat, and temperature change are known for this metal, we can determine its specific heat using the relationship:
q = c × m × ∆T = c × m × (Tfinal – Tinitial)
Substituting the known values:
6640 J = c × (348 g) × (43.6 °C – 22.4 °C)
Solving:
c = ![]() = 0.900 J/(g·°C)
= 0.900 J/(g·°C)
Comparing this value with the values in Table 1, this value matches the specific heat of aluminum, which suggests that the unknown metal may be aluminum. Note that we would need more information to make a definitive determination of the identity.
Check Your Learning
A piece of unknown metal weighs 217 g. When the metal piece absorbs 1.43 kJ of heat, its temperature increases from 24.5 °C to 39.1 °C. Determine the specific heat of this metal, and predict its identity (use Table 1 for reference).
Answer:
c = 0.451 J/(g·°C); the metal is likely to be iron
Chemistry in Real Life: Solar Thermal Energy Power Plants
The sunlight that reaches the earth contains thousands of times more energy than we presently capture. Solar thermal systems provide one possible solution to the problem of converting energy from the sun into energy we can use. Large-scale solar thermal plants have different design specifics, but all concentrate sunlight to heat some substance. The heat “stored” in that substance is then converted into electricity.
The Solana Generating Station in Arizona’s Sonora Desert produces 280 megawatts of electrical power. It uses parabolic mirrors that focus sunlight on pipes filled with a heat transfer fluid (HTF) (Figure 2). The HTF then does two things: It turns water into steam, which spins turbines, which in turn produces electricity, and it melts and heats a mixture of salts, which functions as a thermal energy storage system. After the sun goes down, the molten salt mixture can then release enough of its stored heat to produce steam to run the turbines for 6 hours. Molten salts are used because they possess a number of beneficial properties, including high heat capacities and thermal conductivities.
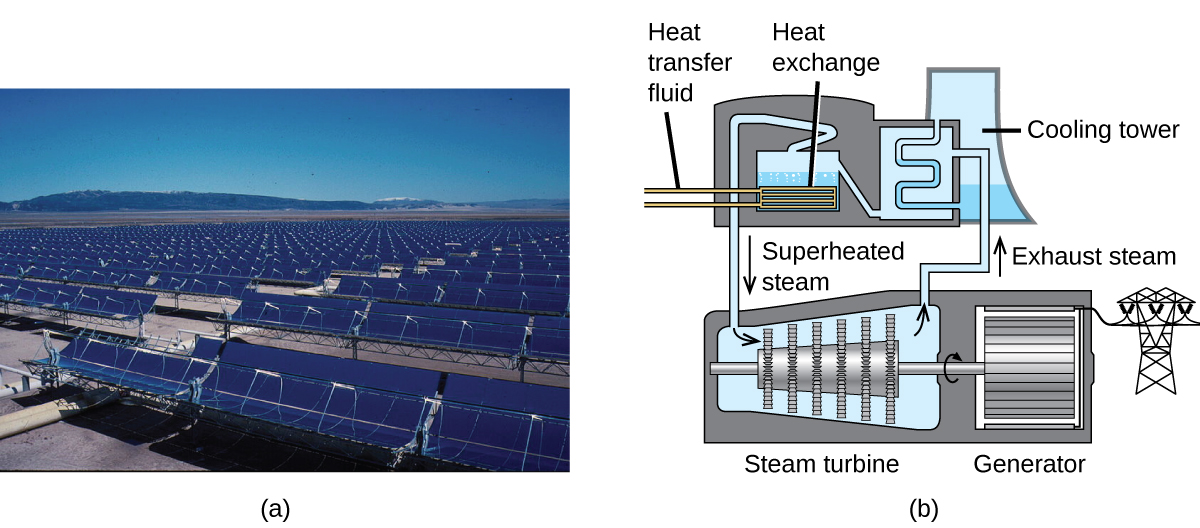
The 377-megawatt Ivanpah Solar Generating System, located in the Mojave Desert in California, is the largest solar thermal power plant in the world (Figure 3). Its 170,000 mirrors focus huge amounts of sunlight on three water-filled towers, producing steam at over 538 °C that drives electricity-producing turbines. It produces enough energy to power 140,000 homes. Water is used as the working fluid because of its large heat capacity and heat of vaporization.

Key Concepts and Summary
Heat capacity is an extensive property of a substance that depends on both the quantity and identity of the substance. The heat capacity describes how much energy is needed to change the temperature of the substance. The specific heat capacity is an intensive property that only depends on the identity of the substance. This quantity is the energy required to raise a specific quantity (usually 1 g) of a substance a certain amount (usually 1 °C or 1 K). The amount of heat absorbed or released by a substance depends directly on these quantities.
Key Equations
- q = c × m × ∆T = c × m × (Tfinal – Tinitial)
Glossary
- heat capacity (C)
- extensive property of a body of matter that represents the quantity of heat required to increase its temperature by 1 degree Celsius (or 1 kelvin)
- specific heat capacity (c)
- intensive property of a substance that represents the quantity of heat required to raise the temperature of 1 gram of the substance by 1 degree Celsius (or 1 kelvin)
Chemistry End of Section Exercises
- A burning match and a bonfire may have the same temperature, yet you would not sit around a burning match on a fall evening to stay warm. Why not?
- Explain the difference between heat capacity and specific heat of a substance.
- Calculate the heat capacity, in joules and in calories per degree, of the following:
- 45.8 g of nitrogen gas
- 1.00 pound of aluminum metal
- How much heat must be added to a 75.0 g iron block with a specific heat of 0.449 J/g·°C to increase its temperature from 25 °C to its melting temperature of 1535 °C?
- How much heat is required to heat a 28.4 g (1 oz) ice cube from −23.0 °C to −1.0 °C?
- If 14.5 kJ of heat were added to 485 g of liquid water, how much would its temperature increase?
- A piece of unknown solid substance weighs 437.2 g, and requires 8460 J to increase its temperature from 19.3 °C to 68.9 °C.
- What is the specific heat of the substance?
- If it is one of the substances found in Table 1, what is its likely identity?
- An aluminum kettle weighs 1.05 kg.
- What is the heat capacity of the kettle?
- How much heat is required to increase the temperature of this kettle from 23.0 °C to 99.0 °C?
- How much heat is required to heat this kettle from 23.0 °C to 99.0 °C if it contains 1.25 L of water (density of 0.997 g/mL and a specific heat of 4.184 J/g·°C)?
- Most people find waterbeds uncomfortable unless the water temperature is maintained at about 85 °F. Unless it is heated, a waterbed that contains 892 L of water cools from 85 °F to 72 °F in 24 hours. Estimate the amount of electrical energy required over 24 hours, in kWh, to keep the bed from cooling. Note that 1 kilowatt-hour (kWh) = 3.6 × 106 J, and assume that the density of water is 1.0 g/mL (independent of temperature). What other assumptions did you make? How did they affect your calculated result (i.e., were they likely to yield “positive” or “negative” errors)?
- The Solana Generating Station in Arizona uses thermal energy from the sun to melt and heat ionic salts – substances that have a high thermal conductivity and specific heat. Explain why these physical properties of molten salts are beneficial for electricity production at night.
Answers to Chemistry End of Section Exercises
- The temperature of 1 gram of burning wood is approximately the same for both a match and a bonfire. This is an intensive property and depends on the material (wood). However, the overall amount of produced heat depends on the amount of material; this is an extensive property. The amount of wood in a bonfire is much greater than that in a match; the total amount of produced heat is also much greater, which is why we can sit around a bonfire to stay warm, but a match would not provide enough heat to keep us from getting cold.
- Heat capacity refers to the heat required to raise the temperature of the mass of the substance by one degree; specific heat refers to the heat required to raise the temperature of one gram of the substance by one degree. Thus, heat capacity is an extensive property, and specific heat is an intensive one.
- (a) 47.6 J/°C; 11.38 cal/°C; (b) 407 J/°C; 97.3 cal/°C
- 5.08 × 104 J
- 1.31 × 103 J
- 7.15 °C
- (a) 0.390 J/g·°C; (b) Copper is a likely candidate.
- (a) 942 J/°C; (b) 7.16 × 104 J; (c) 4.68 × 105 J
- Energy required = 7.5 kWh. We assume that the density of water is 1.0 g/cm3 (1 g/mL) and that it takes as much energy to keep the water at 85 °F as to heat it from 72 °F to 85 °F a difference of 13 oF or 7.2 oC. We also assume that only the water is going to be heated.
- These physical properties allow the sun’s heat to be stored efficiently, which can later be converted into electricity. After the sun goes down, the molten salt mixture can then release enough of its stored heat to produce steam to run the turbines for 6 hours.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

