M13Q8: Relationship between Reaction Rates, Temperature, and Activation Energy; Arrhenius Equation, Orientation Factor

Chem 103 Textbook Team; Chem 104 Textbook Team

M13Q8: Relationship between Reaction Rates, Temperature, and Activation Energy; Arrhenius Equation, Orientation Factor

Learning Objectives

Draw and interpret reaction coordinate diagrams, and identify the transition state(s) on these diagrams.
Apply the Arrhenius equation to illustrate the effects of temperature and activation energy on reaction rate and recognize the reaction characteristics represented by the pre-exponential factor (A).
Describe how collision frequencies and molecular orientations affect reaction rates.

Activation Energy and the Arrhenius Equation

We can use the Arrhenius equation to relate the activation energy and the rate constant, k, of a given reaction:

k = A $e^{^{-\frac{E_{a}}{RT}}}$

In this equation, R is the ideal gas constant, which has a value 8.314 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ , T is temperature in Kelvin scale, E_a is the activation energy in J/mol, and A is a constant called the frequency factor, which is related to the frequency of collisions and the orientation of the reacting molecules.

Both postulates of the collision theory of reaction rates are accommodated in the Arrhenius equation. The frequency factor, A, is related to the rate at which collisions having the correct orientation occur. The exponential term, $e^{^{-\frac{E_{a}}{RT}}}$ , is related to the fraction of collisions providing adequate energy to overcome the activation barrier of the reaction.

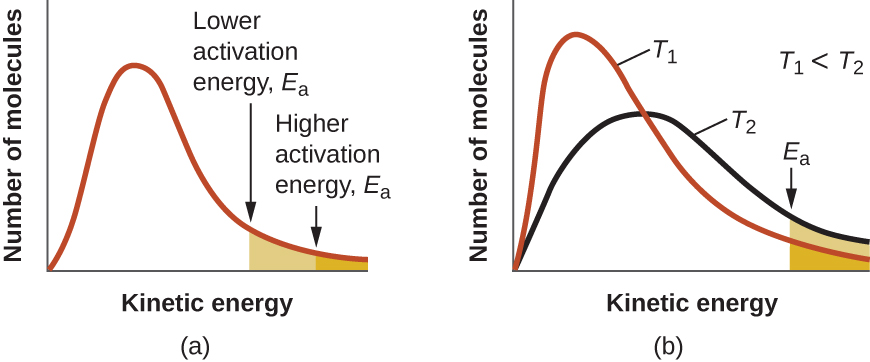
At one extreme, the system does not contain enough energy for collisions to overcome the activation energy barrier. In such cases, no reaction occurs. At the other extreme, the system has so much energy that every collision with the correct orientation can overcome the activation barrier, causing the reaction to proceed. In such cases, the reaction is nearly instantaneous.

The Arrhenius equation describes quantitatively much of what we have already discussed about reaction rates. For two reactions at the same temperature, the reaction with the higher activation energy has the smaller rate constant and the slower rate. The larger value of E_a results in a smaller value for $e^{^{-\frac{E_{a}}{RT}}}$ , reflecting the smaller fraction of molecules with enough energy to react. Alternatively, the reaction with the smaller E_a has a larger fraction of molecules with enough energy to react. This will be reflected as a larger value of $e^{^{-\frac{E_{a}}{RT}}}$ , a larger rate constant, and a faster rate of reaction. An increase in temperature has the same effect as a decrease in activation energy. A larger fraction of molecules has the necessary energy to react (Figure 1), as indicated by an increase in the value of $e^{^{-\frac{E_{a}}{RT}}}$ . The rate constant is also directly proportional to the frequency factor, A. Hence a change in conditions or reactants that increases the number of collisions with a favorable orientation for reaction results in an increase in A and, consequently, an increase in k.

Two graphs are shown each with an x-axis label of “Kinetic energy” and a y-axis label of “Fraction of molecules.” Each contains a positively skewed curve indicated in red that begins at the origin and approaches the x-axis at the right side of the graph. In a, a small area under the far right end of the curve is shaded orange. An arrow points down from above the curve to the left end of this region where the shading begins. This arrow is labeled, “Higher activation energy, E subscript a.” In b, the same red curve appears, and a second curve is drawn in black. It is also positively skewed, but reaches a lower maximum value and takes on a broadened appearance as compared to the curve in red. In this graph, the red curve is labeled, “T subscript 1” and the black curve is labeled, “T subscript 2.” In the open space at the upper right on the graph is the label, “T subscript 1 less than T subscript 2.” As with the first graph, the region under the curves at the far right is shaded orange and a downward arrow labeled “E subscript a” points to the left end of this shaded region. — **Figure 1**. (a) As the activation energy of a reaction decreases, the number of molecules with at least this much energy increases, as shown by the shaded areas. (b) At a higher temperature, T₂, more molecules have kinetic energies greater than E_a, as shown by the yellow shaded area.

A convenient approach to determining E_a for a reaction involves the measurement of k at different temperatures and using of an alternate version of the Arrhenius equation that takes the form of linear equation:

ln k	=	$\left(\dfrac{-E_{a}}{R}\right)\left(\dfrac{1}{T}\right)$	+	ln A
y	=	mx	+	b

Thus, a plot of ln k versus $\dfrac{1}{T}$ gives a straight line with the slope $\dfrac{-E_{a}}{R}$ , from which E_a may be determined. The y-intercept gives the value of ln A.

In many situations, it is possible to obtain a reasonable estimate of the activation energy without going through the entire process of constructing the Arrhenius plot. The slope of the plot is:

$\dfrac{\Delta (\ln k)}{\Delta \frac{1}{T}}$

Slope is also equal to:

$\dfrac{-E_{a}}{R}$

Put together:

$\dfrac{\Delta (\ln k)}{\Delta \frac{1}{T}} = -\dfrac{E_{a}}{R}$

Solving for ln k

Δ(ln k) = $\left(-\dfrac{E_{a}}{R}\right)\left(\Delta{\dfrac{1}{T}}\right)$

Substituting in Δ(ln k) = ln k₂ – ln k₁ and $\Delta \dfrac{1}{T} = \dfrac{1}{T_{2}} - \dfrac{1}{T_{1}}$ , we have:

ln k₂ – ln k₁ = $\left(-{\dfrac{E_{a}}{R}}\right)\left( \dfrac{1}{T_{2}} - \dfrac{1}{T_{1}}\right)$

Note that ln k₂ – ln k₁ = ln $\frac{k_{2}}{k_{1}}$ . Therefore, the equation can also be written as

$\ln \left(\dfrac{k_{2}}{k_{1}}\right) = \left(-{\dfrac{E_{a}}{R}}\right)\left(\dfrac{1}{T_{2}} - \dfrac{1}{T_{1}}\right)$

There are other forms of this equation, depending on how the negative sign is incorporated. (note that $\ln \left(\dfrac{k_{2}}{k_{1}}\right) = - \ln \left(\dfrac{k_{1}}{k_{2}}\right)$ .) For example:

$\ln \dfrac{k_{1}}{k_{2}} = \left({\dfrac{E_{a}}{R}}\right)\left(\dfrac{1}{T_{2}} - \dfrac{1}{T_{1}}\right)$

$\ln \dfrac{k_{2}}{k_{1}} = \left({\dfrac{E_{a}}{R}}\right)\left(\dfrac{1}{T_{1}} - \dfrac{1}{T_{2}}\right)$

Whichever form of the equation you use, be sure to keep careful track of the variables k₁, k₂, T₁, and T₂ (k₁ is measured at T₁, and k₂ is measured at T₂), and place them correctly in the equation.

This equation can be used to give a one-step calculation to obtain a value for the activation energy.

Example 1

Determination of E_a
The variation of the rate constant with temperature for the decomposition of HI(g) to H₂(g) and I₂(g) is given here. What is the activation energy for the reaction?

2 HI(g) → H₂(g) + I₂(g)

T (K)	k (M^-1s^-1)
555	3.52 × 10⁻⁷
575	1.22 × 10⁻⁶
645	8.59 × 10⁻⁵
700	1.16 × 10⁻³
781	3.95 × 10⁻²

Solution
Values of $\frac{1}{T}$ and ln k are:

$\frac{\textbf{1}}{\textbf{T}}$ K^-1	ln k
1.80 × 10⁻³	−14.860
1.74 × 10⁻³	−13.617
1.55 × 10⁻³	−9.362
1.43 × 10⁻³	−6.759
1.28 × 10⁻³	−3.231

Figure 2 is a graph of ln k versus $\frac{1}{T}$ .

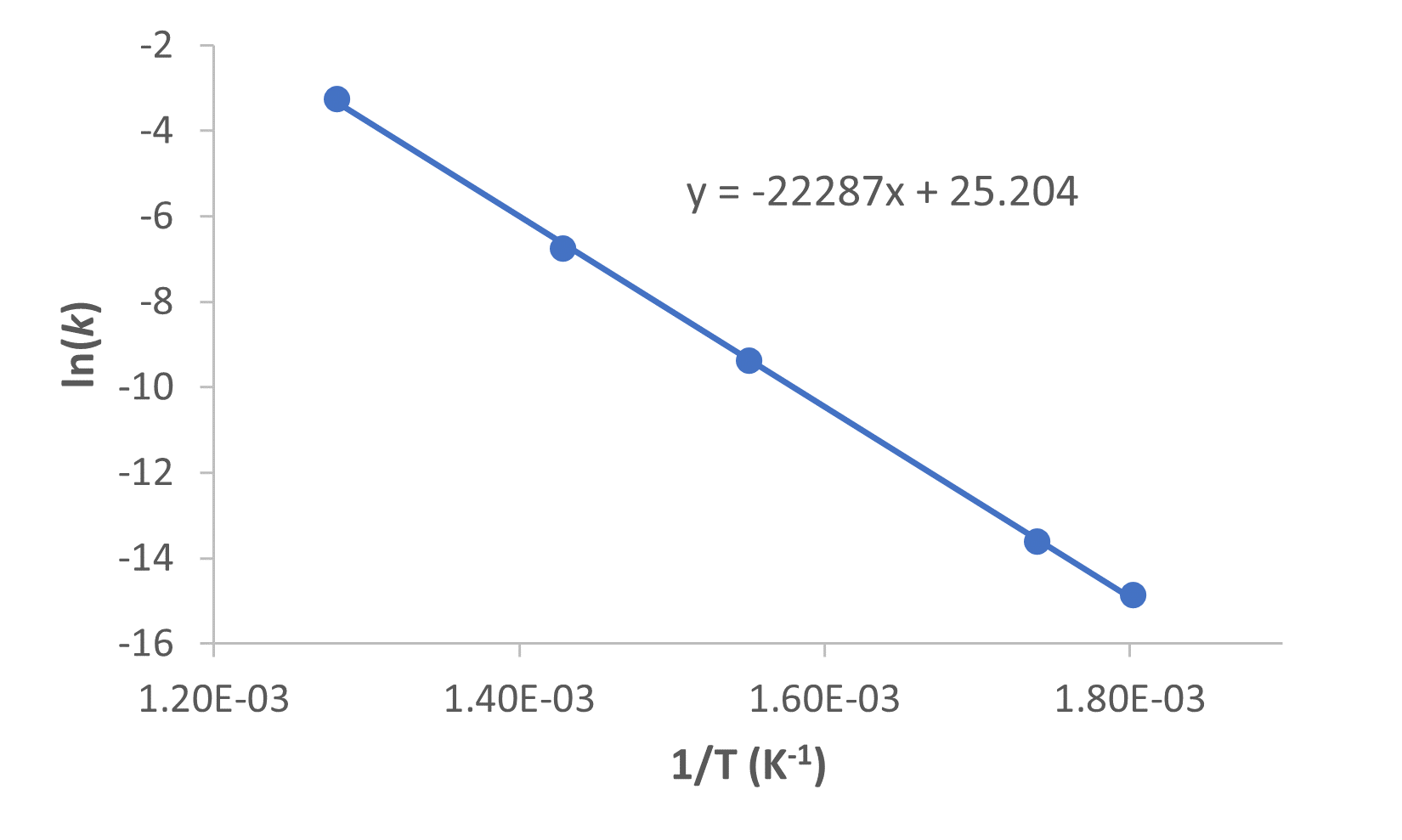
An Arrhenius plot of the data shown in Example 1. The linear fit yields an equation y = -22287x + 25.204 — **Figure 2**. This graph shows the linear relationship between ln k and 1/T for the reaction 2 HI ⟶ H₂ + I₂ according to the Arrhenius equation.

A linear fit of the data gives the slope, from which we can determine the activation energy from the relationship: slope = $\dfrac{-E_{a}}{R}$ :

E_a = -slope × R = -(-2.23 × 10⁴ K) × (8.314 $\frac{\text{J}}{\text{mol} \cdot \text{K}}$ ) = 1.85 × 10⁵ J/mol

Alternatively, we can simply select two data entries to calculate activation energy without needing to graph the data. For example, we can use the first entry and the last entry:

Trial	T (K)	k (M^-1s^-1)
1	555	3.52 × 10⁻⁷
2	781	3.95 × 10⁻²

Plugging the values into the equation

$\ln \left(\dfrac{k_{2}}{k_{1}}\right) = \left(-{\dfrac{E_{a}}{R}}\right)\left(\dfrac{1}{T_{2}} - \dfrac{1}{T_{1}}\right)$

we have:

$\ln \left(\dfrac{3.95 \times 10^{-2}\;\frac{1}{\text{M} \cdot \text{s}}}{3.52 \times 10^{-7}\frac{1}{\text{M} \cdot \text{s}}}\right) = \left(-{\dfrac{E_{a}}{8.314\;\frac{\text{J}}{\text{mol} \cdot \text{K}}}}\right)\left(\dfrac{1}{781\;\text{K}} - \dfrac{1}{555\;\text{K}}\right)$

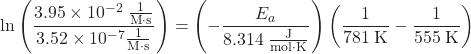
Solving for E_a gives:

11.625 = -(E_a)(-6.27 × 10^-5 mol/J)

E_a = 1.85 × 10⁵ J/mol

This method is effective when a limited number of temperature-dependent rate constants are available for the reaction of interest.

Check Your Learning
The rate constant for the rate of decomposition of N₂O₅ to NO and O₂ in the gas phase is 1.66 M^-1s^-1 at 650 K and 7.39 M^-1s^-1 at 700 K:

2 N₂O₅(g) → 4 NO(g) + 3 O₂(g)

Assuming the kinetics of this reaction are consistent with the Arrhenius equation, calculate the activation energy for this decomposition.

Answer:

113,000 J/mol

Reaction Rate, Activation Energy, and Temperature

The rate constant is directly proportional to temperature and inversely proportion to the activation energy:

k = A $e^{^{-\frac{E_{a}}{RT}}}$

Because the rate constant is directly proportional to the reaction rate, the relationship between rate, activation energy, and temperature can be summarized as follows:

Reactions with values of small E_a (E_a< 15 kJ/mol) are fast and not very temperature sensitive.
Reactions with values of large E_a (E_a > 120 kJ/mol) are slow and very temperature-sensitive.
Many common reactions have E_a in the range of 50-100 kJ/mol. The rates of these reactions more-or-less double every 10°C temperature increase.

Key Concepts and Summary

The Arrhenius equation allows us to calculate the activation energy of a reaction, once a few other variables are known. In the most common form of the Arrhenius equation (k = A $e^{^{-\frac{E_{a}}{RT}}}$ ), the rate constant and frequency factor are variables along with the activation energy and temperature. In the graphable form of the equation (ln k = ( $\frac{-E_{a}}{R}$ )( $\frac{1}{T}$ ) + ln A), multiple rate constants are needed at different temperatures and the slope is related to the activation energy. In the last form of the equation (ln $\frac{k_{2}}{k_{1}}$ = (- ${\frac{E_{a}}{R}}$ )( ${ \frac{1}{T_{2}}}$ – ${ \frac{1}{T_{1}}}$ )), only two rate constants are needed at two different temperatures to calculate the activation energy. To determine which equation to use in a particular situation, focus on the variables that you are given and find the equation that matches those variables.

Key Equations

k = A $e^{^{-\frac{E_{a}}{RT}}}$
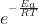
ln k = 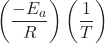$\left(\dfrac{-E_{a}}{R}\right)\left(\dfrac{1}{T}\right)$ + ln A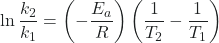
$\ln \dfrac{k_{2}}{k_{1}} = \left(-\dfrac{E_{a}}{R}\right) \left(\dfrac{1}{T_{2}} - \dfrac{1}{T_{1}}\right)$

Glossary

Arrhenius equation: an equation that relates the activation energy and rate constant of a reaction

frequency factor (A): a constant in the Arrhenius equation that is related to the frequency of collisions and the orientation of reacting molecules

Chemistry End of Section Exercises

The rate of a certain reaction doubles for every 10 °C rise in temperature.
1. How much faster does the reaction proceed at 45 °C than at 25 °C?
2. How much faster does the reaction proceed at 95 °C than at 25 °C?
Which of the following graphs best represents the relationship between reaction rate and temperature?
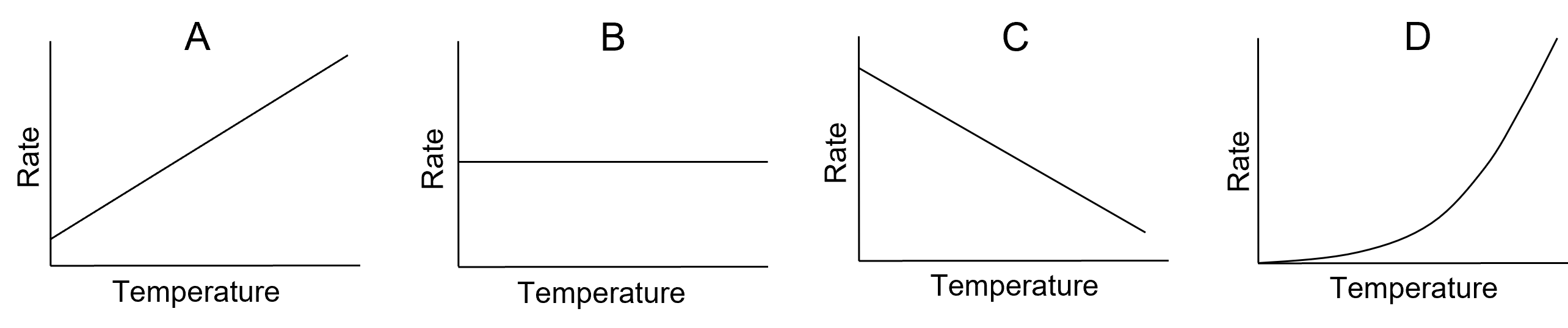
Which of the following statements regarding the Arrhenius equation is correct?
1. A plot of ln k vs. T gives a straight line with a slope equal to –E_a/R.
2. The Arrhenius expression of the rate constant is only valid for first order reactions.
3. The frequency factor, A, has the same units as the rate constant, k.
4. The frequency factor, A, is the same for all reactions.
5. None of the above statements are correct.
The rate constant at 325 °C for the decomposition reaction
C₄H₈ (g) → 2 C₂H₄(g)

is 6.1 × 10^-8 s^-1, and the activation energy is 261 kJ per mole of C₄H₈. Determine the frequency factor for the reaction.
The rate constant for the decomposition of acetaldehyde, CH₃CHO, to methane, CH₄, and carbon monoxide, CO, in the gas phase is 1.1 × 10⁻² M^-1s^-1 at 703 K and 4.95 M^-1s^-1 at 865 K. Determine the activation energy for this decomposition.
An elevated level of the enzyme alkaline phosphatase (ALP) in the serum is an indication of possible liver or bone disorder. The level of serum ALP is so low that it is very difficult to measure directly. However, ALP catalyzes a number of reactions, and its relative concentration can be determined by measuring the rate of one of these reactions under controlled conditions. One such reaction is the conversion of p-nitrophenyl phosphate (PNPP) to p-nitrophenoxide ion (PNP) and phosphate ion. Control of temperature during the test is very important; the rate of the reaction increases 1.47 times if the temperature changes from 30 °C to 37 °C. What is the activation energy for the ALP–catalyzed conversion of PNPP to PNP and phosphate?
Hydrogen iodide, HI, decomposes in the gas phase to produce hydrogen, H₂, and iodine, I₂. The value of the rate constant, k, for the reaction was measured at several different temperatures and the data are shown here:

Temperature (K) k (M⁻¹ s⁻¹)

555 6.23 × 10⁻⁷

575 2.42 × 10⁻⁶

645 1.44 × 10⁻⁴

700 2.01 × 10⁻³

What is the value of the activation energy (in kJ/mol) for this reaction?
Rate constant values at various temperatures were collected for a second order reaction and are plotted in the graph below.
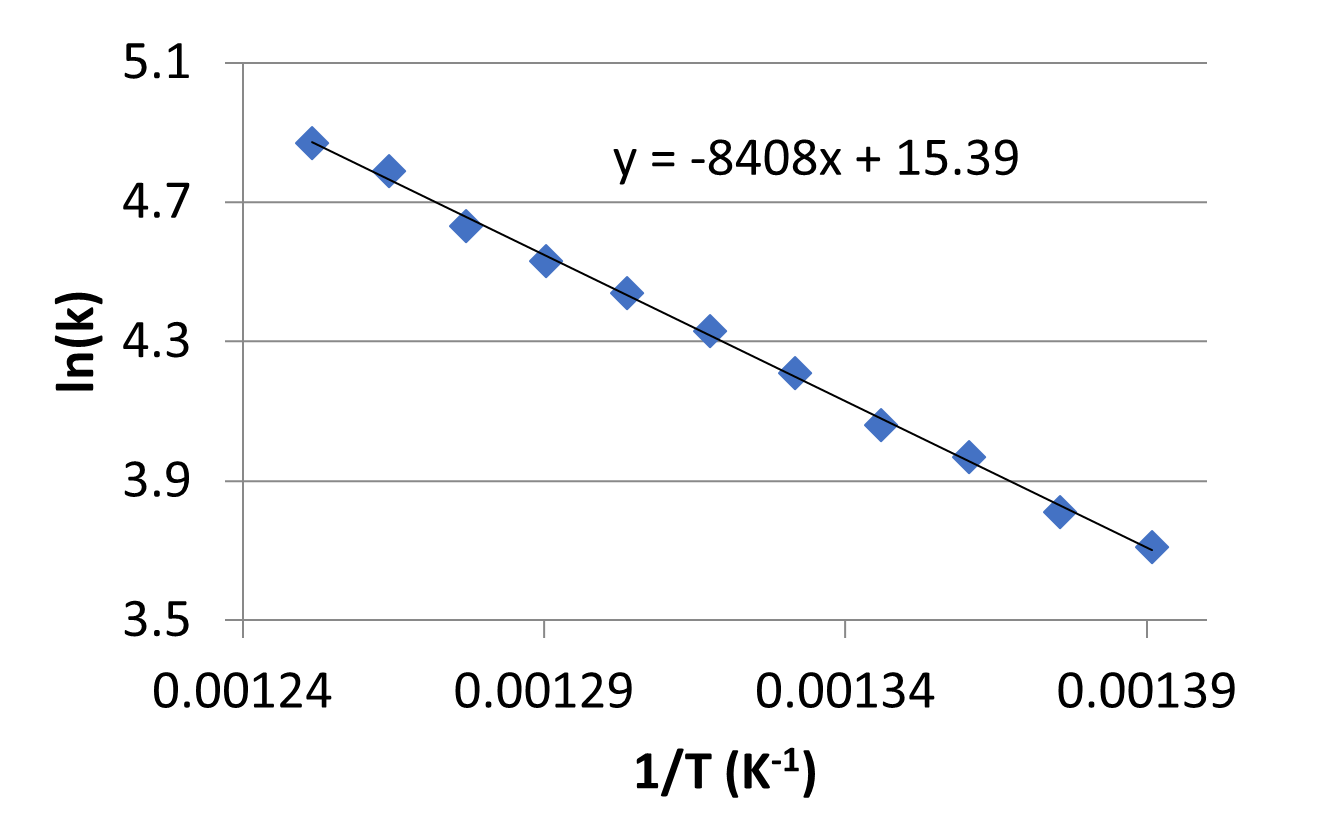
1. What is the activation energy for the reaction? Include units in your answer.
2. What is the frequency factor, A, for this reaction? Include units in your answer.
The rate constant, k, for the decomposition of acetaldehyde is 0.122 s^-1 at 425 °C and 0.789 s^-1 at 535 °C.
CH₃CHO(g) → CH₄(g) + CO(g)
1. What is the activation energy for this reaction?
2. What is the value of the frequency factor at 425 °C?
The hydrolysis of the sugar sucrose to the sugars glucose and fructose,
C₁₂H₂₂O₁₁(s) + H₂O(ℓ) → C₆H₁₂O₆(s) + C₆H₁₂O₆(s)

follows a first-order rate equation for the disappearance of sucrose: Rate = k[C₁₂H₂₂O₁₁].
1. Note that the products of the reaction, glucose and fructose, have the same molecular formulas but differ in the arrangement of the atoms in their molecules. How are these molecules related?
2. In neutral solution, k = 2.1 × 10⁻¹¹ s⁻¹ at 27 °C and 8.5 × 10⁻¹¹ s⁻¹ at 37 °C. Determine the activation energy and the rate constant for this reaction at 47 °C (assuming the kinetics remain consistent with the Arrhenius equation at this temperature).
3. When a solution of sucrose with an initial concentration of 0.150 M reaches equilibrium, the concentration of sucrose is 1.65 × 10⁻⁷M. How long will it take the solution to reach equilibrium at 27 °C in the absence of a catalyst? Because the concentration of sucrose at equilibrium is so low, assume that the reaction is irreversible.
4. Why does assuming that the reaction is irreversible simplify the calculation in part (c)?

Answers to Chemistry End of Section Exercises

(a) 4 times faster; (b) 128 times faster
D
C
3.9 × 10¹⁵ s^-1
190.66 kJ/mol
Remember rate is proportional to k. 43.0 kJ/mol
180. kJ/mol
(a) E_a = 69,910 J/mol; (b) A = 4.8 × 10⁶ M^-1s^-1
(a) E_a = 79.6 kJ/mol; (b) A = 1.11 × 10⁵ s^-1

Left-click here to watch Exercise 9 problem solving video.
(a) They are structural isomers
(b) E_a = 108 kJ/mol; k = 3.15 × 10⁻¹⁰ s⁻¹(c) 1.81 × 10⁸ h or 7.6 × 10⁶ day
(d) Assuming that the reaction is irreversible simplifies the calculation because we do not have to account for any reactant that, having been converted to product, returns to the original state.

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Temperature (K)	k (M⁻¹ s⁻¹)
555	6.23 × 10⁻⁷
575	2.42 × 10⁻⁶
645	1.44 × 10⁻⁴
700	2.01 × 10⁻³