M16Q1: Defining a Buffer; Calculating the pH of a Buffer Solution

Chem 103 Textbook Team; Chem 104 Textbook Team

M16Q1: Defining a Buffer; Calculating the pH of a Buffer Solution

Learning Objectives

Describe, recognize, and provide examples of buffer solutions; identify the components of buffer systems.
| How Buffers Work |
Apply a K_a expression or the Henderson-Hasselbalch equation in order to calculate the pH of a buffer system.
| Henderson-Hasselbalch Equation |

Buffers

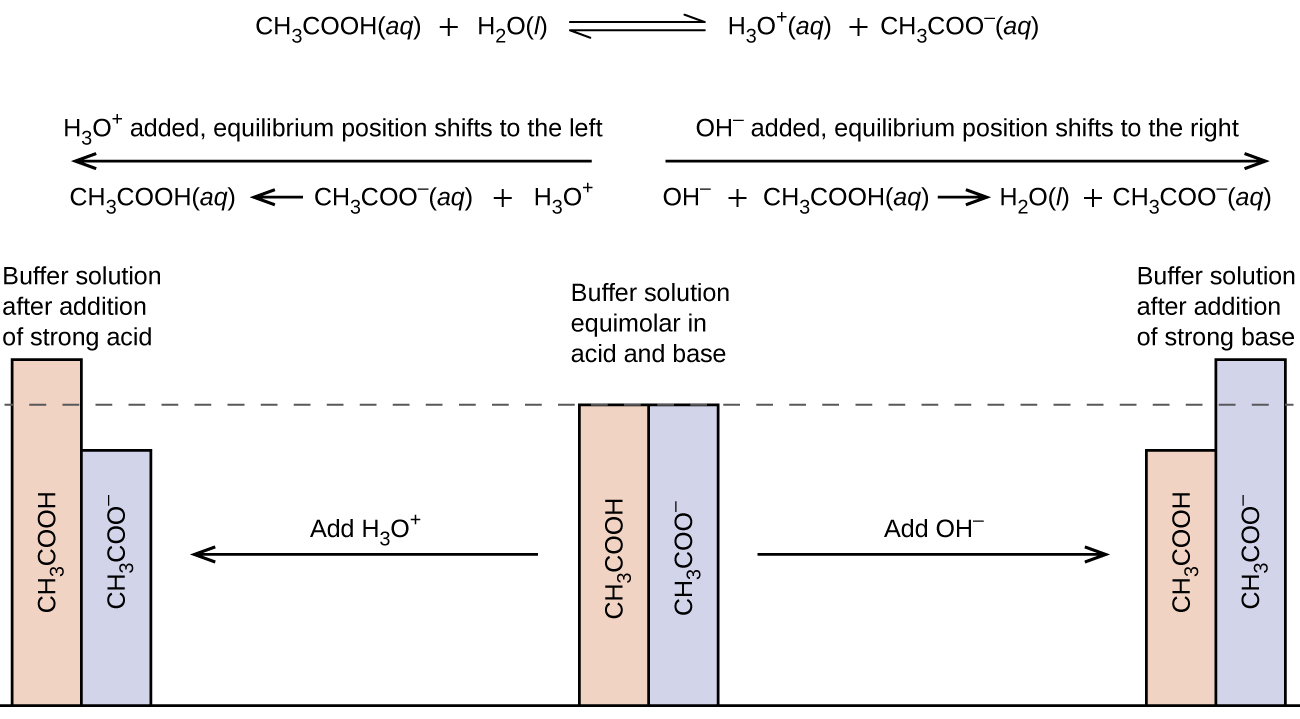
A buffer solution, or a buffer is a solution composed of approximately equal amounts of a dissolved weak acid and weak base conjugate pair. Buffer solutions resist a change in pH when a strong acid or a strong base are added (Figure 1).

A solution of acetic acid and acetate ion (CH₃COOH + CH₃COO^–) is an example of an acidic buffer. A solution of ammonia and ammonium ion (NH₃ + NH₄⁺) is an example of a basic buffer. Both contain both weak acid and weak base, regardless of the resulting pH.

To summarize, both a weak acid and weak base must be present in a buffer solution, and the weak acid and weak base must be conjugate pairs.

Two images are shown. Image a on the left shows two beakers that each contain yellow solutions. The beaker on the left is labeled “Unbuffered” and the beaker on the right is labeled “p H equals 8.0 buffer.” Image b similarly shows 2 beakers. The beaker on the left contains a bright orange solution and is labeled “Unbuffered.” The beaker on the right is labeled “p H equals 8.0 buffer.” — **Figure 1.** (a) The unbuffered solution on the left and the buffered solution on the right have the same pH (pH 8); they are basic, showing the yellow color of the indicator methyl orange at this pH. (b) After the addition of 1 mL of a 0.01-M HCl solution, the buffered solution has not detectably changed its pH but the unbuffered solution has become acidic, as indicated by the change in color of the methyl orange, which turns red at a pH of about 4. (credit: modification of work by Mark Ott)

Chemistry in Real Life: Blood and Buffers

Blood is an important example of a buffered solution, with the principal acid and ion responsible for the buffering action being carbonic acid, H₂CO₃, and the bicarbonate ion, HCO₃^–.

H₂CO₃(aq) + H₂O(ℓ) ⇌ HCO₃^–(aq) + H₃O⁺(aq)

The pH of human blood remains very near 7.35, that is, slightly basic. Variations are usually less than 0.1 of a pH unit. A change of 0.4 of a pH unit is likely to be fatal.

How Buffers Work

A mixture of acetic acid and sodium acetate is a buffer because it contains both the weak acid and its conjugate base, assuming their quantities are similar. If we add a strong acid, the acetate ions will react with the hydronium ions created by the strong acid to produce acetic acid and water (as seen below). Acetic acid is a weak acid, which will cause the pH to decrease by a very small amount compared to the addition of a strong acid to pure water.

CH₃COO^–(aq) + H₃O⁺(aq) → CH₃COOH(aq) + H₂O(ℓ)

Conversely, if we add a strong base, such as sodium hydroxide, the hydroxide ions react with the acetic acid to produce acetate ions and water. Acetate ions are a weak base, which cause the pH to increase by a very small amount compared to the addition of a strong base to water.

CH₃COOH(aq) + OH^–(aq) → CH₃COO^–(aq) + H₂O(ℓ)

These two examples show how a buffer is able to resist pH changes even when a strong acid or base are added (Figure 2).

This figure begins with a chemical reaction at the top: C H subscript 3 C O O H ( a q ) plus H subscript 2 O ( l ) equilibrium arrow H subscript 3 O superscript positive sign ( a q ) plus C H subscript 3 C O O superscript negative sign ( a q ). Below this equation are two arrows: one pointing left and other pointing right. The arrow pointing left has this phrase written above it, “H subscript 3 O superscript positive sign added, equilibrium position shifts to the left.” Below the arrow is the reaction: C H subscript 3 C O O H ( a q ) left-facing arrow C H subscript 3 C O O superscript negative sign ( a q ) plus H subscript 3 O superscript positive sign. The arrow pointing right has this phrase written above it, “O H subscript negative sign added, equilibrium position shifts to the right.” Below the arrow is the reaction: O H superscript negative sign plus C H subscript 3 C O O H ( a q ) right-facing arrow H subscript 2 O ( l ) plus C H subscript 3 C O O superscript negative sign ( a q ). Below all the text is a figure that resembles a bar graph. In the middle are two bars of equal height. One is labeled, “C H subscript 3 C O O H,” and the other is labeled, “C H subscript 3 C O O superscript negative sign.” There is a dotted line at the same height of the bars which extends to the left and right. Above these two bars is the phrase, “Buffer solution equimolar in acid and base.” There is an arrow pointing to the right which is labeled, “Add O H superscript negative sign.” The arrow points to two bars again, but this time the C H subscript 3 C O O H bar is shorter than that C H subscript 3 C O O superscript negative sign bar. Above these two bars is the phrase, “Buffer solution after addition of strong base.” From the middle bars again, there is an arrow that points left. The arrow is labeled, “Add H subscript 3 O superscript positive sign.” This arrow points to two bars again, but this time the C H subscript 3 C O O H bar is taller than the C H subscript 3 C O O superscript negative sign bar. These two bars are labeled, “Buffer solution after addition of strong acid.” — **Figure 2.** This diagram shows the buffer action of these reactions.

A mixture of ammonia and ammonium chloride is basic because the K_b for ammonia is greater than the K_a for the ammonium ion. It is a buffer because it also contains a weak acid and a weak base, assuming their quantities are close to equal. If we add a strong acid, the ammonia molecules will react with the hydronium ions to produce ammonium and water (as seen below), converting a strong acid into a weak acid.

NH₃(aq) + H₃O⁺(aq) → NH₄⁺(aq) + H₂O(ℓ)

If we add a strong base, the ammonium ions will react with the hydroxide ions to produce ammonia and water (as seen below), converting a strong base into a weak base.

NH₄⁺(aq) + OH^–(aq) → NH₃(aq) + H₂O(ℓ)

The Henderson-Hasselbalch Equation

The Henderson-Hasselbalch equation is used to calculate the pH of buffer solutions from the ionization constant (K_a) of the relevant weak acid and the concentrations of both the weak acid and its conjugate base in solution. This equation is derived from the equilibrium expression for a weak acid dissociating in water, as can be seen below.

The ionization-constant expression for a solution of a weak acid can be written as:

K_a = $\dfrac{[\text{H}_{3}\text{O}^{+}][\text{A}^{-}]}{[\text{HA}]}$

After rearranging to solve for [H₃O⁺]:

[H₃O⁺] = K_a × $\dfrac{[\text{HA}]}{[\text{A}^{-}]}$

Taking the negative logarithm of both sides of this equation:

-log[H₃O⁺] = -log(K_a) + (-log $\dfrac{[\text{HA}]}{[\text{A}^{-}]}$ )

which can be written as

pH = pK_a + log $\dfrac{[\text{A}^{-}]}{[\text{HA}]}$

where pK_a is the negative of the common logarithm of the ionization constant of the weak acid (pK_a = −log K_a). The Henderson-Hasselbalch equation always uses the K_a of the conjugate acid/base pair.

Example 1

Calculating the pH of Buffer Solutions
Calculate the pH of an acetic acid buffer solution with a K_a = 1.8 x 10^-5, [CH₃COONa] = 0.25 M and [CH₃COOH] = 0.50 M.

Solution

Using the given K_a and concentrations, plug all the values into the Henderson-Hasselbalch equation:

pH = pK_a + log $\dfrac{[\text{A}^{-}]}{[\text{HA}]}$

pH = -log(1.8 × 10^-5) + log $\left(\dfrac{0.25\;\text{M}}{0.50\;\text{M}}\right)$ = 4.74 – 0.301 = 4.44

Check Your Learning
Calculate the pH of an ammonia buffer solution with a K_b of 1.8 x 10^-5, [NH₃] = 0.70 M and [NH₄⁺] = 0.40 M.

Answer:

pH = 9.49 (Hint: Don’t forget to calculate the K_a!)

Chemistry in Real Life: Lawrence Joseph Henderson and Karl Albert Hasselbalch

Lawrence Joseph Henderson (1878–1942) was an American physician, biochemist and physiologist, to name only a few of his many pursuits. He obtained a medical degree from Harvard and then spent 2 years studying in Strasbourg, then a part of Germany, before returning to take a lecturer position at Harvard. He eventually became a professor at Harvard and worked there his entire life. He discovered that the acid-base balance in human blood is regulated by a buffer system formed by the dissolved carbon dioxide in blood. He wrote an equation in 1908 to describe the carbonic acid-carbonate buffer system in blood. Henderson was broadly knowledgeable; in addition to his important research on the physiology of blood, he also wrote on the adaptations of organisms and their fit with their environments, on sociology and on university education. He also founded the Fatigue Laboratory, at the Harvard Business School, which examined human physiology with specific focus on work in industry, exercise, and nutrition.

In 1916, Karl Albert Hasselbalch (1874–1962), a Danish physician and chemist, shared authorship in a paper with Christian Bohr in 1904 that described the Bohr effect, which showed that the ability of hemoglobin in the blood to bind with oxygen was inversely related to the acidity of the blood and the concentration of carbon dioxide. The pH scale was introduced in 1909 by another Dane, Sørensen, and in 1912, Hasselbalch published measurements of the pH of blood. In 1916, Hasselbalch expressed Henderson’s equation in logarithmic terms, consistent with the logarithmic scale of pH, and the Henderson-Hasselbalch equation was born.

View information on the buffer system encountered in natural waters.

Key Concepts and Summary

Buffer solutions, which contain a conjugate weak acid and weak base pair, resist a change in pH when a strong acid or a strong base are added. When a strong acid is added, the weak base reacts converting the strong acid into a weak acid (resulting in a small pH decrease). When a strong base is added, the weak acid reacts converting the strong base into a weak base (resulting in a small pH increase).

The Henderson-Hasselbalch equation can be used to calculate the pH of a buffer solution, both before and after a strong acid or strong base addition. This equation is: pH = pKa + log $\dfrac{[\text{A}^{-}]}{[\text{HA}]}$ , where pH = -log[H₃O⁺], pKa = -log(K_a), [A^–] = moles or concentration of the weak base, [HA] = moles or concentration of the weak acid.

Key Equations

pH = pKa + log $\dfrac{[\text{A}^{-}]}{[\text{HA}]}$

Glossary

buffer: solution composed of approximately equal amounts of a dissolved weak acid and weak base conjugate pair

Henderson-Hasselbalch equation: used to calculate the pH of buffer solutions from the ionization constant (K_a) and the concentrations of both the weak acid and its conjugate base in solution.

Chemistry End of Section Exercises

What is a buffer?
Write the chemical equation that represents a buffer comprised of equal amounts of the acid H₃PO₄ and a salt of its conjugate base NaH₂PO₄. Explain why the pH does not change significantly when a small amount of (a) an acid or (b) a base is added to this solution.
Write the chemical equation that represents a buffer comprised of equal amounts of the base NH₃ and a salt of its conjugate acid NH₄Cl. Explain why the pH does not change significantly when a small amount of (a) an acid or (b) a base is added to this solution.
Which of the following combinations could be used to create a buffer solution? Explain briefly.
1. HNO₃ and HNO₂
2. HNO₂ and NO₃^–
3. NO₂^– and HNO₂
4. NH₄⁺ and NH₃
5. NH₃ and CH₃NH₂
What is the effect (increase, decrease, no effect) on the concentration of formic acid (HCOOH), hydronium ion, and formate ion (HCOO^–) when the following are added to a buffer solution of equal concentrations of formic acid and sodium formate:
1. HCl
2. KHCOO
3. NaCl
4. KOH
5. HCOOH
What is the effect (increase, decrease, no effect) on the pH when the following are added to a buffer solution of equal concentrations of NaH₂PO₄ and Na₂HPO₄:
1. HCl
2. K₂HPO₄
3. NaCl
4. KOH
5. NaH₂PO₄
What is the pH of a solution that is 0.25 M CH₃COOH and 0.030 M NaCH₃COO. The K_a for CH₃COOH is 1.8 × 10^-5.
What is the pH of a solution that is 0.075 M HNO₂ and 0.030 M NaNO₂. The K_a for HNO₂ is 7.4 × 10^-4.
What is the pH of a buffer that is 0.125 M CH₃NH₂ and 0.130 M CH₃NH₃Cl. The K_b for CH₃NH₂ is 5.0 × 10^-4.
What is the pH of a buffer that is 1.25 M NH₃ and 0.78 M NH₄Cl. The K_b for NH₃ is 1.77 × 10^-5.
Calculate the pH of a solution that contains 0.25 M benzoic acid, C₆H₅COOH, and 0.15 M sodium benzoate, C₆H₅COONa. K_a(C₆H₅COOH) = 6.5 × 10^-5.
A solution is prepared by mixing 500.0 mL of 0.10 M NaOCl and 250.0 mL of 0.40 M HOCl. What is the pH of this solution? K_a(HOCl) = 3.2 × 10^-8.
Which of the following solutions will have a pH greater than 7.00? Select all that apply.
1. 0.10 M sodium acetate, CH₃COONa
2. A solution that contains equal concentrations of HCN and KCN (K_a(HCN) = 6.2 × 10^-10)
3. 1.0 M trimethylammonium chloride, (CH₃)₃NHCl

Answers to Chemistry End of Section Exercises

A buffer is a solution that resists change in pH when small amounts of a strong acid or base are added. The solution is comprised of approximately equal concentrations of a weak acid and its conjugate base (or a weak base and its conjugate acid).
H₃PO₄(aq) + H₂O(ℓ) ⇌ H₂PO₄^–(aq) + H₃O⁺(aq); Note that the Na⁺ is a spectator ion and is not included
(a) Added acid, H₃O⁺, is removed primarily by reacting with the base, H₂PO₄^–, by the reaction: H₃O⁺(aq) + H₂PO₄^–(aq) → H₃PO₄(aq) + H₂O(ℓ)
(b) Added base, OH^–, is removed primarily by reacting with the acid, H₃PO₄, by the reaction: OH^–(aq) + H₃PO₄(aq) → H₂PO₄^–(aq) + H₂O(ℓ)
NH₄⁺(aq) + H₂O(ℓ) ⇌ NH₃(aq) + H₃O⁺(aq); Note that the Cl^– is a spectator ion and is not included
(a) Added acid, H₃O⁺, is removed primarily by reacting with the base, NH₃, by the reaction: H₃O⁺(aq) + NH₃(aq) → NH₄⁺(aq) + H₂O(ℓ)
(b) Added base, OH^–, is removed primarily by reacting with the acid, NH₄⁺, by the reaction: OH^–(aq) + NH₄⁺(aq) → NH₃(aq) + H₂O(ℓ)
C and D. Buffers are mixtures of a weak acid and its conjugate base.
Buffer reaction: HCOOH(aq) + H₂O(ℓ) ⇌ HCOO^–(aq) + H₃O⁺(aq)
Consider the effects using Le Châtelier’s Principle:
(a) HCl adds H₃O⁺ to the reaction, pushing the equilibrium toward the reactants. This causes [HCOOH] to increase, [H₃O⁺] to increase, and [HCOO^–] to decrease.
(b) KHCOO is a soluble ionic compound and will dissolve upon addition to the solution. The K⁺ is a spectator ion and will not affect the equilibrium. Additional HCOO^– will shift the equilibrium toward the reactants, causing the [HCOOH] to increase, [H₃O⁺] to decrease, and [HCOO^–] to increase.
(c) NaCl will dissolve, adding Na⁺ and Cl^– ions to the solution. Neither of these will effect the equilibrium and so the concentrations will be unchanged.
(d) KOH will dissolve upon addition, adding K⁺ and OH^– ions to the solution. The OH- ions will react with the H₃O⁺, decreasing the H₃O⁺ concentration and causing the equilibrium to shift to toward the products. The [HCOOH] will decrease, [H₃O⁺] will decrease, and [HCOO^–] will increase.
(e) Adding HCOOH will shift the equilibrium toward the products. The [HCOOH] will decrease, [H₃O⁺] will increase, and [HCOO^–] will increase.
Buffer reaction: H₂PO₄^–(aq) + H₂O(ℓ) ⇌ HPO₄^2-(aq) + H₃O⁺(aq)
(a) pH will decrease
(b) pH will increase
(c) pH will be unchanged
(d) pH will increase
(e) pH will decrease
3.82
2.73
10.68
9.45
3.97
7.19
A and B

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.