M7Q1: Waves and the Electromagnetic Spectrum

Introduction

This section explores the properties of light. Visible light and other forms of electromagnetic radiation play important roles in chemistry since they can be used to infer the energies of electrons within atoms and molecules. Much of modern technology is based on electromagnetic radiation. For example, radio waves from a mobile phone, X-rays used by dentists, the energy used to cook food in your microwave, the radiant heat from red-hot objects, and the light from your television screen are forms of electromagnetic radiation that all exhibit wavelike behavior. By understanding the phenomena of light, you will grasp the inner workings of many of our modern technologies. Included in this section are worked examples, sample problems, and a glossary.

Learning Objectives for Waves and the Electromagnetic Spectrum

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

Properties of Waves

A wave is an oscillation or periodic movement that can transport energy from one point in space to another. Common examples of waves are all around us. Shaking the end of a rope transfers energy from your hand to the other end of the rope, dropping a pebble into a pond causes waves to ripple outward along the water’s surface, and the expansion of air that accompanies a lightning strike generates sound waves (thunder) that can travel outward for several miles. In each of these cases, kinetic energy is transferred through matter (the rope, water, or air) while the matter remains essentially in place.

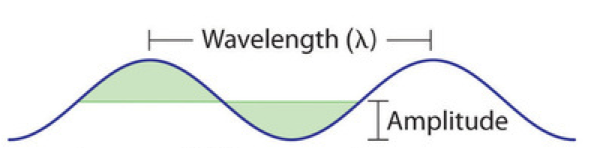
All waves are characterized by a wavelength (denoted by λ, the lowercase Greek letter lambda), a frequency (denoted by ν, the lowercase Greek letter nu), and an amplitude. As can be seen in Figure 1, the wavelength is the distance between two consecutive peaks or troughs in a wave (measured in meters in the SI system). The frequency is the number of wave cycles that pass a specified point in space in a specified amount of time (in the SI system, this time is measured in seconds). A cycle corresponds to one complete wavelength. The unit for frequency, therefore, is expressed as cycles per second (s−1), also referred to as hertz (Hz). The amplitude corresponds to the magnitude of the wave’s displacement and so, in Figure 1, this corresponds to one-half the height between the peaks and troughs.

A wave is shown. The wavelength is labeled as the distance between two peaks of the wave. The amplitude is labeled as the distance from the trough of the wave to the point halfway between the peak and the trough. And the frequency is labeled as 1 Hz and spans an entire wavelength, indicating that 1 wavelength passes in 1 second, giving a frequency of 1 Hz.
Figure 1. Two important properties of a wave — wavelength (λ) and amplitude.

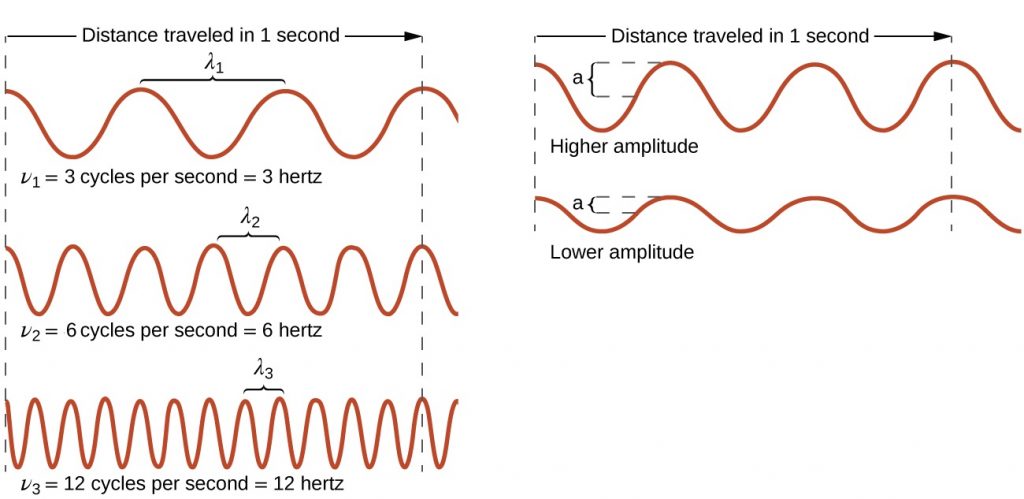
As can be seen in Figure 2, the properties of a wave are related. On the left side of Figure 2, all waves have the same amplitude, but the wave on top only completes 3 cycles per second, and therefore has a frequency of 3 Hz. The wave on the bottom completes 12 cycles in the same amount of time (1 second), and therefore has a frequency of 12 Hz. In order to complete 4 times as many cycles in the same timeframe, the wavelength of the bottom wave must be shorter than the wavelength of the top wave (in fact, it must be 4 times shorter) and assuming that the waves are traveling at the same speed. This produces an inverse relationship between wavelength and frequency—as wavelength decreases, frequency increases. Note that this relationship does not depend on the amplitude of the wave. On the right side of Figure 2, you can see that waves with the same wavelength and frequency can have different amplitudes. The amplitude is related to the intensity of the wave, which for light is the brightness, and for sound is the loudness.

This figure has two parts. On the left side, we see the relationship between wavelength and frequency. Two vertical dotted lines are drawn and the distance between them is labeled “Distance traveled in 1 second”. Below this label are three waves. The top wave completes 3 cycles between the two vertical dotted lines and is labeled as “nu 1 equals 3 cycles per second equals 3 hertz”. The wavelength of this wave is labeled as lambda 1. The middle wave completes 6 cycles between the two vertical dotted lines and is labeled as “nu 2 equals 6 cycles per second equals 6 hertz”. The wavelength of this wave is labeled as lambda 2. The bottom wave completes 12 cycles between the two vertical dotted lines and is labeled as “nu 3 equals 12 cycles per seconds equals 12 hertz”. The wavelength of this wave is labeled as lambda 3. The second part of the figure has two vertical dotted lines and the distance between them is labeled “Distance traveled in 1 second”. Below this are two waves. The top wave is labeled as “High amplitude” and has a high amplitude. The bottom wave is labeled as “low amplitude” and has a low amplitude. These two waves complete the same number of cycles in 1 second and therefore have the same frequency, even if their amplitudes are different.
Figure 2. The wavelength and frequency of a wave are related: The longer the wavelength, the fewer wavelengths completed in 1 second.

Not all waves are traveling waves. Standing waves (also known as stationary waves) remain constrained within some region of space. The simplest example of a standing wave is a one-dimensional wave associated with a vibrating string that is held fixed at its two end points. Figure 3 shows the four lowest-energy standing waves for a vibrating string at a particular amplitude. Although the string’s motion lies mostly within a plane, the wave itself is considered to be one dimensional, since it lies along the length of the string. The motion of string segments in a direction perpendicular to the string length generates the waves and so the amplitude of the waves is visible as the maximum displacement of the curves seen in Figure 3. The key observation from the figure is that only those waves having an integer number, n, of half-wavelengths between the end points can form. A system with fixed end points such as this restricts the number and type of the possible waveforms. Another important observation is that the waves displaying more than one-half wavelength all have one or more points between the two end points that are not in motion. These special points with zero amplitude are called nodes. The energies of the standing waves with a given amplitude in a vibrating string increase with the number of half-wavelengths, n. Since the number of nodes is n – 1, the energy can also be said to depend on the number of nodes, generally increasing as the number of nodes increases.

This figure shows four one-dimensional standing waves. The waves are shown in a tan color and are composed of curves to represent standing waves that can be generated using string. The first image at the top of the figure shows a single long wave with no nodes, or points where the string appears to cross between the endpoints at the left and right sides of the figure. The second diagram just below shows a single node at the center of the wave, which divides the wave into two identical halves to the left and right. The third diagram shows two nodes, dividing the image into three identical parts to the left, center, and right. Similarly, the last image at the bottom of the figure shows three nodes, dividing the image into four identical parts.
Figure 3. A vibrating string shows some one-dimensional standing waves. Since the two end points of the string are held fixed, only waves having an integer number of half-wavelengths can form. The points on the string between the end points that are not moving and have zero amplitude are called the nodes.

Demonstration: Nodes in standing waves

Set up. The following video shows a demonstration of a standing wave created using a rope attached to a drill. As the drill bit rotates, the rope forms a standing wave. You will notice that the number of nodes, peaks, and troughs in the wave will change with the energy input from the drill.

Explanation. Starting at the lowest drill speed, there was one half wavelength between the stationary point on the left side of the rope and the drill bit on the right side of the rope. With increased energy from the drill, the number of wavelengths between the two ends increases, as do the number of nodes.

The Electromagnetic Spectrum

The nature of light has been a subject of inquiry since antiquity. In the seventeenth century, Isaac Newton performed experiments with lenses and prisms and was able to demonstrate that white light consists of the individual colors of the rainbow combined together. Newton explained his optics findings in terms of a “corpuscular” view of light, in which light was composed of streams of extremely tiny particles traveling at high speeds according to Newton’s laws of motion. Others in the seventeenth century, such as Christiaan Huygens, had shown that optical phenomena such as reflection and refraction could be equally well explained in terms of light as waves traveling at high speed through a medium called “luminiferous aether” that was thought to permeate all space.

Early in the nineteenth century, Thomas Young demonstrated that light passing through narrow, closely spaced slits produced interference patterns that could not be explained in terms of Newtonian particles but could be easily explained in terms of waves. Later in the nineteenth century, after James Clerk Maxwell developed his theory of electromagnetic radiation and showed that light was the visible part of a vast spectrum of electromagnetic waves, the particle view of light became thoroughly discredited. By the end of the nineteenth century, scientists viewed the physical universe as roughly comprising two separate domains: matter composed of particles moving according to Newton’s laws of motion, and electromagnetic radiation consisting of waves governed by Maxwell’s equations.

Today, these domains are referred to as classical mechanics and classical electrodynamics (or classical electromagnetism), respectively. Although there were a few physical phenomena that could not be explained within this framework, scientists at that time were so confident of the overall soundness of this framework that they viewed these aberrations as puzzling paradoxes that would ultimately be resolved somehow within this framework. As we shall see, these paradoxes led instead to an entirely new framework that intimately connects both particles and waves at a fundamental level called wave-particle duality, which has superseded the classical view and marked the beginning of a revolution in science.

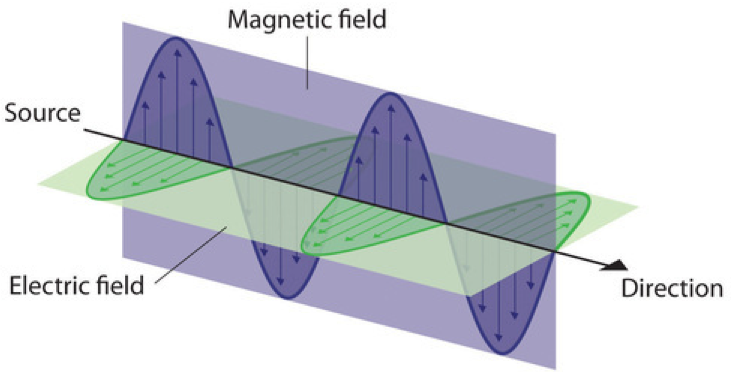
Water waves transmit energy through space by the periodic oscillation of matter (the water). But waves need not be restricted to travel through matter. As Maxwell showed, electromagnetic waves consist of an electric field oscillating in step with a perpendicular magnetic field, both of which are perpendicular to the direction of travel (Figure 4). The properties of waves—λ, ν, and amplitude—that were used to describe waves in matter also apply to forms of electromagnetic radiation. Electromagnetic waves have wavelengths that fall within an enormous range—wavelengths of kilometers (103 m) to picometers (10−12 m) have been observed. Frequencies commonly have units of megahertz (1 MHz = 1 × 106 Hz) and gigahertz (1 GHz = 1 × 109 Hz), indicating that 1 × 106 or 1 × 109 wavelengths pass a single point in one second.

This image has a black arrow pointing toward the right. On the left side of the arrow is the label "source" and on the right side of the arrow is labeled "direction". The black line of this arrow marks the central axis for two perpendicular waves. One is oriented vertically in the plane of the page and one is oriented into and out of the page. These waves are labeled "magnetic field" and "electric field", respectively.
Figure 4. The nature of electromagnetic radiation. All forms of electromagnetic radiation consist of perpendicular oscillating electric and magnetic fields.

Electromagnetic waves travel through a vacuum at a constant speed of 2.998 × 108 m/s, the speed of light (denoted by c). The product of a wave’s wavelength (λ) and its frequency (ν), λν, is the speed of the wave. Thus, for electromagnetic radiation in a vacuum:

c = 2.998 × 108 m/s = λν

Notice that the units of c in this equation are m/s. For this equation, the wavelength must be in units of meters and the frequency must be in units of Hz (or 1/s) so that when you multiply λν you end up with m × \frac{1}{s} = \frac{m}{s}, which is the unit of the speed of light. Make sure that your units appropriately cancel using dimensional analysis, as always.

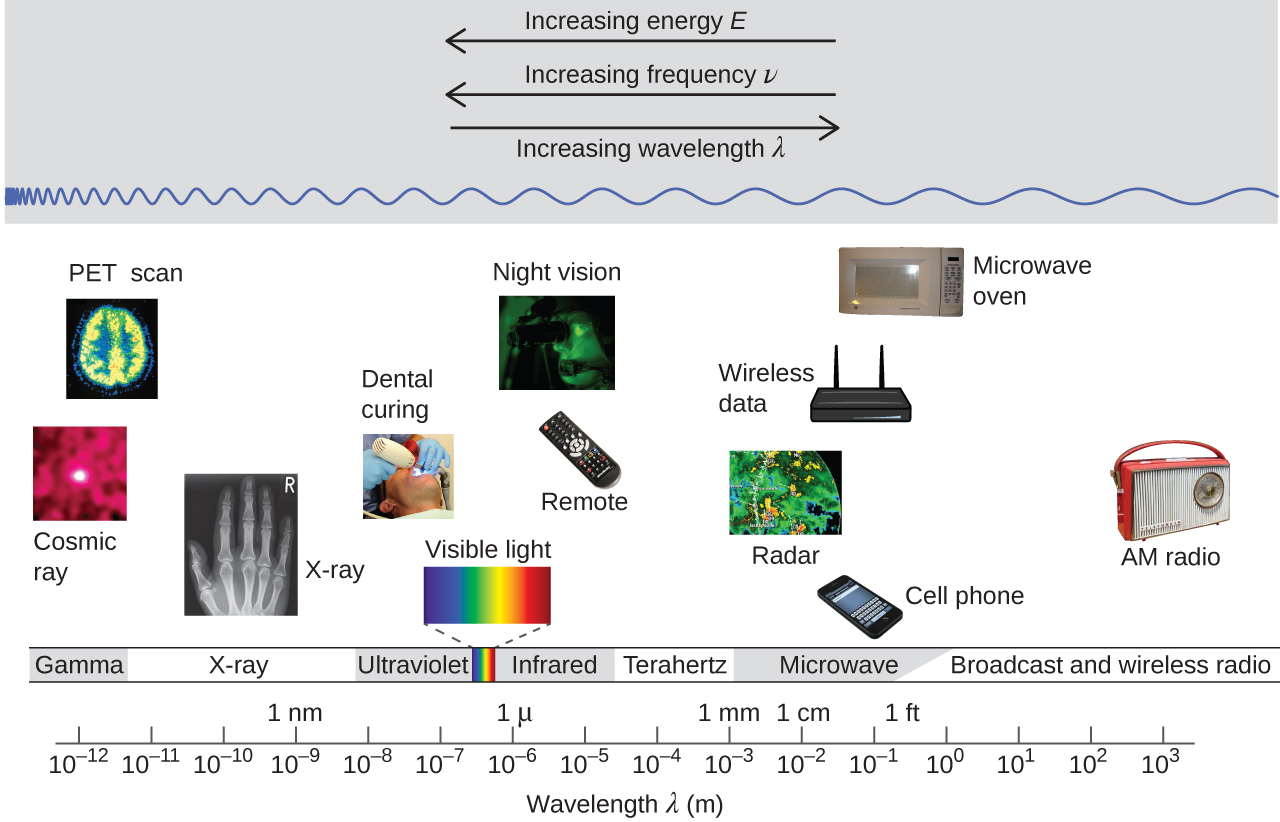
This equation is another demonstration of the inverse relationship between wavelength and frequency: As the wavelength increases, the frequency must decrease so that the speed remains constant. The inverse proportionality is illustrated in Figure 5. This figure also shows the electromagnetic spectrum—the range of all types of electromagnetic radiation. Each of the various colors of visible light has specific frequencies and wavelengths associated with them, and you can see that visible light makes up only a small portion of the electromagnetic spectrum. Because the technologies developed to work in various parts of the electromagnetic spectrum are different, for reasons of convenience and historical legacies, different units are typically used for different parts of the spectrum. For example, radio waves are usually specified as frequencies (typically in units of MHz), while the visible region is usually specified in wavelengths (typically in units of nm or angstroms).

The figure includes a portion of the electromagnetic spectrum which extends from gamma radiation at the far left through x-ray, ultraviolet, visible, infrared, terahertz, and microwave to broadcast and wireless radio at the far right. At the top of the figure, inside a grey box, are three arrows. The first points left and is labeled, “Increasing energy E.” A second arrow is placed just below the first which also points left and is labeled, “Increasing frequency nu.” A third arrow is placed just below which points right and is labeled, “Increasing wavelength lambda.” Inside the grey box near the bottom is a blue sinusoidal wave pattern that moves horizontally through the box. At the far left end, the waves are short and tightly packed. They gradually lengthen moving left to right across the figure, resulting in significantly longer waves at the right end of the diagram. Beneath the grey box are a variety of photos aligned above the names of the radiation types and a numerical scale that is labeled, “Wavelength lambda ( m ).” This scale runs from 10 superscript negative 12 meters under gamma radiation increasing by powers of ten to a value of 10 superscript 3 meters at the far right under broadcast and wireless radio. X-ray appears around 10 superscript negative 10 meters, ultraviolet appears in the 10 superscript negative 8 to 10 superscript negative 7 range, visible light appears between 10 superscript negative 7 and 10 superscript negative 6, infrared appears in the 10 superscript negative 6 to 10 superscript negative 5 range, teraherz appears in the 10 superscript negative 4 to 10 superscript negative 3 range, microwave infrared appears in the 10 superscript negative 2 to 10 superscript negative 1 range, and broadcast and wireless radio extend from 10 to 10 superscript 3 meters. Labels above the scale are placed to indicate 1 n m at 10 superscript negative 9 meters, 1 micron at 10 superscript negative 6 meters, 1 millimeter at 10 superscript negative 3 meters, 1 centimeter at 10 superscript negative 2 meters, and 1 foot between 10 superscript negative 1 meter and 10 superscript 0 meters. A variety of images are placed beneath the grey box and above the scale in the figure to provide examples of related applications that use the electromagnetic radiation in the range of the scale beneath each image. The photos on the left above gamma radiation show cosmic rays and a multicolor PET scan image of a brain. A black and white x-ray image of a hand appears above x-rays. An image of a patient undergoing dental work, with a blue light being directed into the patient's mouth is labeled, “dental curing,” and is shown above ultraviolet radiation. Between the ultraviolet and infrared labels is a narrow band of violet, indigo, blue, green, yellow, orange, and red colors in narrow, vertical strips. From this narrow band, two dashed lines extend a short distance above to the left and right of an image of the visible spectrum. The image, which is labeled, “visible light,” is just a broader version of the narrow bands of color in the label area. Above infrared are images of a television remote and a black and green night vision image. At the left end of the microwave region, a satellite radar image is shown. Just right of this and still above the microwave region are images of a cell phone, a wireless router that is labeled, “wireless data,” and a microwave oven. Above broadcast and wireless radio are two images. The left most image is a black and white medical ultrasound image. A wireless AM radio is positioned at the far right in the image, also above broadcast and wireless radio.
Figure 5. Portions of the electromagnetic spectrum are shown in order of decreasing frequency and increasing wavelength. Examples of some applications for various wavelengths include positron emission tomography (PET) scans, X-ray imaging, remote controls, wireless Internet, cellular telephones, and radios. (credit “Cosmic ray”: modification of work by NASA; credit “PET scan”: modification of work by the National Institute of Health; credit “X-ray”: modification of work by Dr. Jochen Lengerke; credit “Dental curing”: modification of work by the Department of the Navy; credit “Night vision”: modification of work by the Department of the Army; credit “Remote”: modification of work by Emilian Robert Vicol; credit “Cell phone”: modification of work by Brett Jordan; credit “Microwave oven”: modification of work by Billy Mabray; credit “Ultrasound”: modification of work by Jane Whitney; credit “AM radio”: modification of work by Dave Clausen)

Demonstration: Elements have characteristic emission spectra

Set up. A flame test is a method used to detect the presence of certain elements in a sample, primarily metals. Samples are exposed to a gas flame and produce a characteristic emission spectrum. We can qualitatively observe the emission spectrum by noting the different colors that are produced when each sample is introduced into the flame (e.g., the lithium sample looks red). Another way of performing this test, as shown in the demonstration below, is to use a spectrometer (sometimes referred to as a spectrophotometer).

In the demonstration below, you will see the reading by the spectrometer in the upper right-hand quadrant of the video. In this spectrum, the x axis displays wavelength (from 350 nm to 950 nm) and the y axis records intensity. You’ll notice that before any samples are introduced into the flame, there are already peaks in the emission spectrum resulting from the color of the flame itself (these peaks occur around 590 nm [tallest], 675 nm [medium height], and 770 nm [shortest]). As samples are introduced (see the label in the lower center of the video), these peaks will change height and new peaks will appear as the flame color changes. The time-stamps with good views of the flame and spectrum are provided below so that you can pause the video to inspect how the spectrum changes.

Explanation. The qualitative results for the flame test are:

  • Lithium produces a red flame (pause the video ~0:26 to observe the spectrum).
  • Boron produces a green flame (~0:36 to observe the spectrum).
  • Sodium produces a yellow flame (~0:44 to observe the spectrum).
  • Potassium produces a purple flame (~0:55 to observe the spectrum).
  • Calcium produces a red flame (~1:06 to observe the spectrum).
  • Copper produces a green flame (~1:13 to observe the spectrum).
  • Strontium produces a scarlet flame (~1:23 to observe the spectrum).
  • Barium produces a yellow-green flame (~1:33 to observe the spectrum).

While the qualitative data (i.e., our perception of the color of the flames) limits the identification of samples based on a flame test, using a spectrometer to record the wavelengths of light produced when each sample is introduced into a flame provides a way to characterize unknown samples.

Example 1

Determining the Frequency and Wavelength of Radiation
A sodium streetlight gives off yellow light that has a wavelength of 589 nm (1 nm = 1 × 10−9 m). What is the frequency of this light?

Solution
We can rearrange the equation c = λν to solve for the frequency:

ν = \dfrac{c}{\lambda}

Since c is expressed in meters per second, we must also convert 589 nm to meters.

ν = \left(\dfrac{2.998 \times 10^8 \;\rule[0.5ex]{1em}{0.1ex}\hspace{-0.9em}\text{m s}^{-1}}{589 \;\rule[0.5ex]{1.4em}{0.1ex}\hspace{-1.4em}\text{nm}}\right) \left(\dfrac{1 \times 10^9 \;\rule[0.5ex]{1.4em}{0.1ex}\hspace{-1.4em}\text{nm}}{1\;\rule[0.5ex]{1em}{0.1ex}\hspace{-0.9em}\text{m}}\right) = 5.09 × 1014 s-1

Check Your Learning
One of the frequencies used to transmit and receive cellular telephone signals in the United States is 850 MHz. What is the wavelength in meters of these radio waves?

Answer:

0.353 m = 35.3 cm

Chemistry in Real Life: Wireless Communication

This figure consists of three cell phone tower images. The first involves a structure that uses a significant degree of scaffolding. The second image includes a tower with what appears to be a base that is essentially a large pole that branches out at the very top. The third image shows a cell phone tower that appears to be disguised as a palm tree.
Figure 6. Radio and cell towers are typically used to transmit long-wavelength electromagnetic radiation. Increasingly, cell towers are designed to blend in with the landscape, as with the Tucson, Arizona, cell tower (right) disguised as a palm tree. (credit left: modification of work by Sir Mildred Pierce; credit middle: modification of work by M.O. Stevens)

Many valuable technologies operate in the radio (3 kHz-300 GHz) frequency region of the electromagnetic spectrum. At the low frequency (low energy, long wavelength) end of this region are AM (amplitude modulation) radio signals (540-2830 kHz) that can travel long distances. FM (frequency modulation) radio signals are used at higher frequencies (87.5-108.0 MHz). In AM radio, the information is transmitted by varying the amplitude of the wave. In FM radio, by contrast, the amplitude is constant and the instantaneous frequency varies (Figure 7).

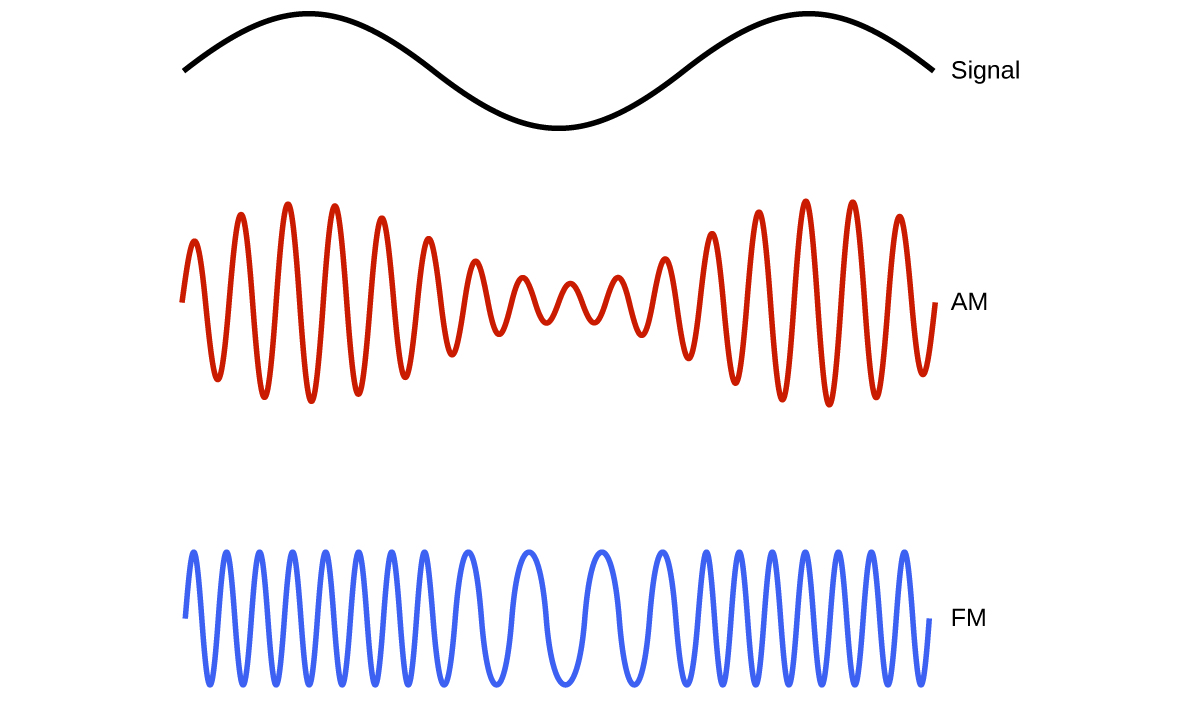
This figure shows 3 wave diagrams. The first wave diagram is in black and shows two crests, indicates a consistent distance from peak to trough, and has one trough in its span across the page. The label, “Signal,” appears to the right. Just below this, a wave diagram is shown in red. The wave includes sixteen crests, but the distance from the peaks to troughs of consecutive waves varies moving across the page. The peak to trough distance is greatest in the region below the peaks of the black wave diagram, and the distance from peak to trough is similarly least below the trough of the black wave diagram. This red wave diagram is labeled, “A M.” The third wave diagram is shown in blue. The distance from peak to trough of consecutive waves is constant across the page, but the peaks and troughs are more closely packed in the region below the peaks of the black wave diagram at the top of the figure. The peaks and troughs are relatively widely spaced below the trough region of the black wave diagram. This blue wave diagram is labeled “F M.”
Figure 7. This schematic depicts how amplitude modulation (AM) and frequency modulation (FM) can be used to transmit a radio wave.

Other technologies also operate in the radio-wave portion of the electromagnetic spectrum. For example, 4G cellular telephone signals are approximately 880 MHz, while Global Positioning System (GPS) signals operate at 1.228 and 1.575 GHz, local area wireless technology (Wi-Fi) networks operate at 2.4 to 5 GHz, and highway toll sensors operate at 5.8 GHz. The frequencies associated with these applications are convenient because such waves tend not to be absorbed much by common building materials.

Key Concepts and Summary

Waves are described by their wavelength (λ), frequency (ν), and amplitude. These terms can be used to describe waves in matter and electromagnetic waves. Light and other forms of electromagnetic radiation move through a vacuum with a constant speed, c, of 2.998 × 108 m/s. The speed of light in a vacuum is not affected by the frequency or wavelength of the light (e.g., blue light moves as fast as red light in a vacuum). This radiation shows wavelike behavior and is an example of a traveling wave. Wavelength and frequency are inversely related: As one increases, the other decreases.

Key Equations

  • c = 2.998 × 108 m/s = λν  

Glossary

amplitude
extent of the displacement caused by a wave (for sinusoidal waves, it is one-half the difference from the peak height to the trough depth, and the intensity is proportional to the square of the amplitude)
electromagnetic radiation
energy transmitted by waves that have an electric-field component and a magnetic-field component
electromagnetic spectrum
range of energies that electromagnetic radiation can comprise, including radio, microwaves, infrared, visible, ultraviolet, X-rays, and gamma rays; since electromagnetic radiation energy is proportional to the frequency and inversely proportional to the wavelength, the spectrum can also be specified by ranges of frequencies or wavelengths
frequency (ν)
number of wave cycles (peaks or troughs) that pass a specified point in space per unit time
hertz (Hz)
the unit of frequency, which is the number of cycles per second, s−1
intensity
property of wave-propagated energy related to the amplitude of the wave, such as brightness of light or loudness of sound
node
any point of a standing wave with zero amplitude
standing wave
(also, stationary wave) localized wave phenomenon characterized by discrete wavelengths determined by the boundary conditions used to generate the waves; standing waves are inherently quantized
wave
oscillation that can transport energy from one point to another in space
wavelength (λ)
distance between two consecutive peaks or troughs in a wave

Chemistry End of Section Exercises

  1. An FM radio station found at 103.1 on the FM dial broadcasts at a frequency of 1.031 × 108 s−1 (103.1 MHz). What is the wavelength of these radio waves in meters?
  2. FM-95, an FM radio station, broadcasts at a frequency of 9.51 × 107 s−1 (95.1 MHz). What is the wavelength of these radio waves in meters?
  3. The laser on a Blu-ray player has a wavelength of 405 nm. In what region of the electromagnetic spectrum is this radiation? What is its frequency?
  4. The emission spectrum of cesium contains two lines whose frequencies are (a) 3.45 × 1014 Hz and (b) 6.53 × 1014 Hz. What are the wavelengths of the two lines? What color are the lines?
  5. When rubidium ions are heated to a high temperature, two lines are observed in its line spectrum at wavelengths (a) 7.9 × 10−7 m and (b) 4.2 × 10−7 m. What are the frequencies of the two lines? What color do we see when we heat a rubidium compound?
  6. Select all the false statement about electromagnetic radiation.
    1. Microwaves have shorter wavelengths than γ-rays.
    2. Red light has lower energy than blue light.
    3. Electromagnetic radiation with wavelength of 1 m is classified as radio waves.
    4. UV rays have greater frequency than X-rays.
  7. True or False: Grass is green because chlorophyll in the leaves absorbs green light.
  8. True or False: Red light has longer wavelength than radio waves.
  9. The sunlight that reaches the surface of our planet contains UV radiation between 280 – 400 nm.  Many sunscreens contain ingredients to block UV-B radiation (280 – 315 nm) but not UV-A radiation (315 – 400 nm). Explain why UV-B radiation is more dangerous than UV-A radiation.

Answers to Chemistry End of Section Exercises

  1. 2.908 m
  2. 3.15 m
  3. Visible region; 7.40 × 1014 Hz
  4. (a) λ = 8.69 × 10−7 m; (b) λ = 4.59 × 10−7 m; The color of (a) is red; (b) is blue.
  5. (a) 3.8 × 1014 Hz; (b) 7.1 × 1014 Hz; The color of (a) is red; (b) is blue.
  6. A and D
  7. False
  8. False
  9. UV-B radiation has higher energy than UV-A radiation, and this higher energy radiation can damage skin cells to potentially lead to skin cancers.
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.