M5Q3: Gas Density

Introduction

In this section, we will rearrange the ideal gas equation so that we can determine density and molar mass of a gas. These calculations demonstrate the versatility and capacity of the ideal gas law to aid in determining experimental conditions, such as pressure or temperature, and the unknown identity and density of a gas. This section includes worked examples and sample problems.

Learning Objectives for Gas Density

| Key Concepts and Summary | End of Section Exercises |

Density of a Gas

Recall that the density of any substance is its mass divided by its volume, ρ = \dfrac{\text{m}}{\text{V}}. (Note, you may see the usage of “d” instead of “ρ” as a symbol representation for density.)

If we can determine the mass of some volume of a gas, we will get its density. The density of an unknown gas can be used to determine its molar mass and thereby assist in its identification. The ideal gas law, PV = nRT, provides us with a means of deriving such a mathematical formula to relate the density of a gas to its volume in the derivation shown in Example 1.

Molar Mass of a Gas

Another useful application of the ideal gas law involves the determination of molar mass. By definition, the molar mass of a substance is the ratio of its mass in grams, m, to its amount in moles, n:

Μ = \dfrac{\text{grams of substance}}{\text{moles of substance}} = \dfrac{m}{n}

The ideal gas equation can be rearranged to isolate n:

n = \dfrac{PV}{RT}

and then combined with the molar mass equation to yield:

Μ  =  \dfrac{mRT}{PV}

This equation can be used to derive the molar mass of a gas from measurements of its pressure, volume, temperature, and mass.

Example 1

Derivation of a Density Formula from the Ideal Gas Law
Use PV  =  nRT to derive a formula for the density of gas in g/L

Solution

  1. PV = nRT
  2. Rearrange to get (mol/L):  \dfrac{n}{V} = \dfrac{P}{RT}
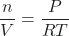
  3. Multiply each side of the equation by the molar mass, Μ.  When moles are multiplied by Μ in g/mol, g are obtained:  (Μ)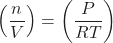\left(\dfrac{n}{V}\right) = \left(\dfrac{P}{RT}\right)(Μ)
  4. g/L = ρ = \dfrac{PM}{RT}

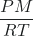
The resulting equation relates the density of a gas (g/L) to its pressure (atm), molar mass, (g/mole) and temperature (K).

Check Your Learning
A gas was found to have a density of 0.0847 g/L at 17.0 °C and a pressure of 760 torr. What is its molar mass? What is the gas?

Answer:

ρ = \dfrac{PM}{RT}

0.0847 g/L = 760 torr × \dfrac{1 \;\rule[0.5ex]{1.8em}{0.1ex}\hspace{-1.8em}\text{atm}}{760 \;\rule[0.5ex]{1.8em}{0.1ex}\hspace{-1.8em}\text{torr}} \times \dfrac{M}{0.0821 \frac{\text{L}\cdot\rule[0.3ex]{1.35em}{0.1ex}\hspace{-1.35em}\text{atm}}{\text{mol}\cdot\rule[0.4ex]{0.6em}{0.1ex}\hspace{-0.6em}\text{K}} \times 290 \;\rule[0.6ex]{0.8em}{0.1ex}\hspace{-0.8em}\text{K}}

Μ = 2.02 g/mol; therefore, the gas must be hydrogen (H2, 2.02 g/mol)

We must specify both the temperature and the pressure of a gas when calculating its density because the number of moles of a gas (and thus the mass of the gas) in a liter changes with temperature or pressure. Gas densities are often reported at STP (standard pressure and temperature conditions, which are 1 atm and 273 K, respectively).

Example 2

Empirical/Molecular Formula Problems Using the Ideal Gas Law and Density of a Gas
Cyclopropane, a gas once used with oxygen as a general anesthetic, is composed of 85.7% carbon and 14.3% hydrogen by mass. Find the empirical formula. If 1.56 g of cyclopropane occupies a volume of 1.00 L at 0.984 atm and 50 °C, what is the molecular formula for cyclopropane?

Solution
Strategy: First solve the empirical formula problem using methods discussed earlier. Assume 100 g and convert the percentage of each element into grams. Determine the number of moles of carbon and hydrogen in the 100-g sample of cyclopropane. Divide by the smallest number of moles to relate the number of moles of carbon to the number of moles of hydrogen. In the last step, realize that the smallest whole number ratio is the empirical formula:

85.7 g C × \dfrac{1\;\text{mol C}}{12.01 \;\text{g C}} = 7.136 mol C

14.3 g H × \dfrac{1\;\text{mol H}}{1.01 \;\text{g H}} = 14.158 mol H

so

\dfrac{7.136}{7.136} = 1.00 mol C

\dfrac{14.158}{7.136} = 1.98 mol H

Empirical formula is CH2 [empirical mass (EM) of 14.03 g/empirical unit].

Next, use the density equation related to the ideal gas law to determine the molar mass:

ρ = \dfrac{PM}{RT}

\dfrac{1.56\;\text{g}}{1.00 \;\text{L}} = 0.984 atm × \dfrac{M}{0.0821 \;\frac{\text{L} \cdot \text{atm}}{\text{mol} \cdot \text{K}} \times 323 \;\text{K}}

Μ = 42.0 g/mol,   \dfrac{M}{\text{EM}} = \dfrac{42.0}{14.03} = 2.99

So (3)(CH2) = C3H6 (molecular formula)

Check Your Learning
Acetylene, a fuel used in welding torches, is comprised of 92.3% C and 7.7% H by mass. Find the empirical formula. If 1.10 g of acetylene occupies of volume of 1.00 L at 1.15 atm and 59.5 °C, what is the molecular formula for acetylene?

Answer:

Empirical formula, CH; Molecular formula, C2H2

Example 3

Determining the Molar Mass of a Volatile Liquid
The approximate molar mass of a volatile liquid can be determined by:

  1. Heating a sample of the liquid in a flask with a tiny hole at the top, which converts the liquid into gas that may escape through the hole
  2. Removing the flask from heat at the instant when the last bit of liquid becomes gas, at which time the flask will be filled with only gaseous sample at ambient pressure
  3. Sealing the flask and permitting the gaseous sample to condense to liquid, and then weighing the flask to determine the sample’s mass (see Figure 1)
This figure shows four photos each connected by a right-facing arrow. The first photo shows a glass flask with aluminum foil covering the top sitting on a scale. The scale reads 89.516. The second photo shows a syringe being inserted into the flask through the aluminum foil covering. The third photo shows the glass flask being inserted into a beaker of water. The water appears to be heated at 100. The fourth photo shows the glass flask being weighed again. This time the scale reads 89.512.
Figure 1. When the volatile liquid in the flask is heated past its boiling point, it becomes gas and drives air out of the flask. At tl⟶g, the flask is filled with volatile liquid gas at the same pressure as the atmosphere. If the flask is then cooled to room temperature, the gas condenses and the mass of the gas that filled the flask, and is now liquid, can be measured. (credit: modification of work by Mark Ott)

Using this procedure, a sample of chloroform gas weighing 0.494 g is collected in a flask with a volume of 129 cm3 at 99.6 °C when the atmospheric pressure is 742.1 mm Hg. What is the approximate molar mass of chloroform?

Solution
Since Μ = \dfrac{m}{n} and n = \dfrac{PV}{RT}, substituting and rearranging gives

Μ = \dfrac{mRT}{PV}

then

Μ = \dfrac{mRT}{PV} = \dfrac{(0.494 \;\text{g}) \times (0.08206 \;\frac{\text{L} \cdot \text{atm}}{\text{mol} \cdot \text{K}}) \times (372.8 \;\text{K)}}{0.976 \;\text{atm} \times 0.129\;\text{L}} = 120 g/mol

Check Your Learning
A sample of phosphorus that weighs 3.243 × 10−2 g exerts a pressure of 31.89 kPa in a 56.0-mL bulb at 550 °C. What are the molar mass and molecular formula of phosphorus vapor?

Answer:

124 g/mol P4

Key Concepts and Summary

The ideal gas law can be used to derive a number of convenient equations relating directly measured quantities to properties of interest for gaseous substances and mixtures. Appropriate rearrangement of the ideal gas equation may be made to permit the calculation of gas densities and molar masses.

Chemistry End of Section Exercises

  1. What is the density of laughing gas, dinitrogen monoxide, N2O, at a temperature of 325 K and a pressure of 113.0 kPa?
  2. Calculate the density of Freon 12 (CF2Cl2), at 30.0 °C and 0.954 atm.
  3. Which is more dense at the same temperature and pressure, dry air or air saturated with water vapor? Explain.
  4. What is the molar mass of a gas if 0.281 g of the gas occupies a volume of 125 mL at a temperature 126 °C and a pressure of 777 torr?
  5. How could you show experimentally that the molecular formula of propene is C3H6, not CH2?
  6. The density of a certain gaseous fluoride of phosphorus is 3.93 g/L at STP. Calculate the molar mass of this compound and determine its molecular formula.
  7. Consider this question: What is the molecular formula of a compound that contains 39% C, 45% N, and 16% H if 0.157 g of the compound occupies l25 mL with a pressure of 99.5 kPa at 22 °C?
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  8. One molecule of hemoglobin will combine with four molecules of oxygen. If 1.0 g of hemoglobin combines with 1.53 mL of oxygen at body temperature (37 °C) and a pressure of 743 torr, what is the molar mass of hemoglobin?
  9. An unidentified chemical is a carcinogen and volatile organic compound with the empirical formula C6H4Cl. The vapor of this chemical is analyzed at 33.0 °C and 0.988 atm, and it is found to have a density of 8.77 g/L.
    1. Determine the molar mass of the gas.
    2. Determine the molecular formula of the compound.
  10. As an ideal gas sample in a glass flask is heated from 100 °C to 200 °C, will the following properties increase, decrease, or remain the same?
    1. Pressure
    2. Volume
    3. Number of moles
    4. Density

Answers to Chemistry End of Section Exercises

  1. 1.84 g/L
  2. 4.64 g/L
  3. Dry air is more dense at the same temperature and pressure. The molar mass of H2O (18 g/mol) is less than that of N2 (28 g/mol) and O2 (32 g/mol). Therefore, the overall density of air saturated with water vapor is less dense.
  4. 72.0 g/mol
  5. M = mRT/PV. If we can measure the mass, the pressure, and temperature of a volume of a gas, we can determine its density. From which, the molar mass of propene can be determined.
  6. 88.0 g/mol; PF3
  7. (a) Determine the empirical formula based on the percent composition. Then use the gas density equation to determine the molar mass, from which the molecular formula can be obtained.
    (b) CNH5
  8. 68,000 g/mole
  9. (a) 223 g/mol; (b) C12H8Cl2
  10. (a) increase; (b) remain the same; (c) remain the same; (d) remain the same
    Left-click here to watch Exercise 10 problem solving video.

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.