M5Q2: Stoichiometry Involving Gases

Introduction

The study of the chemical behavior of gases was part of the basis of perhaps the most fundamental chemical revolution in history. French nobleman Antoine Lavoisier, widely regarded as the “father of modern chemistry,” changed chemistry from a qualitative to a quantitative science through his work with gases. He discovered the law of conservation of matter, discovered the role of oxygen in combustion reactions, determined the composition of air, explained respiration in terms of chemical reactions, and more. He was a casualty of the French Revolution, guillotined in 1794. Regarding his death, mathematician and astronomer Joseph-Louis Lagrange said, “It took the mob only a moment to remove his head; a century will not suffice to reproduce it.”[1]

Chemical stoichiometry is used to answer many questions chemists have in regards to how much of a substance can be produced or consumed during a reaction. Typically these questions are answered with moles or grams of a given substance. However, we can also answer this question another way: with volumes of gases. We can use the ideal gas equation to relate the pressure, volume, temperature, and number of moles of a gas. We can then deal with mixtures of different gases, and calculate amounts of substances in reactions involving gases. This section will integrate concepts of stoichiometry you have already learned with properties of gases as related to the ideal gas law.

Learning Objectives for Stoichiometry Involving Gases

| Key Concepts and Summary | Glossary | End of Section Exercises |

Chemical Stoichiometry and Gases

Chemical stoichiometry describes the quantitative relationships between reactants and products in chemical reactions.

We have previously measured quantities of reactants and products using masses for solids, and volumes in conjunction with the molarity for solutions; now we can also use gas volumes to indicate quantities. If we know the volume, pressure, and temperature of a gas, we can use the ideal gas equation to calculate how many moles of the gas are present. If we know how many moles of a gas are involved, we can calculate the volume of a gas at any temperature and pressure.

Avogadro’s Law Revisited

Sometimes we can take advantage of a simplifying feature of the stoichiometry of gases that solids and solutions do not exhibit: all gases that show ideal behavior contain the same number of molecules in the same volume (at the same temperature and pressure). Thus, the ratios of volumes of gases involved in a chemical reaction are given by the coefficients in the equation for the reaction, provided that the gas volumes are measured at the same temperature and pressure.

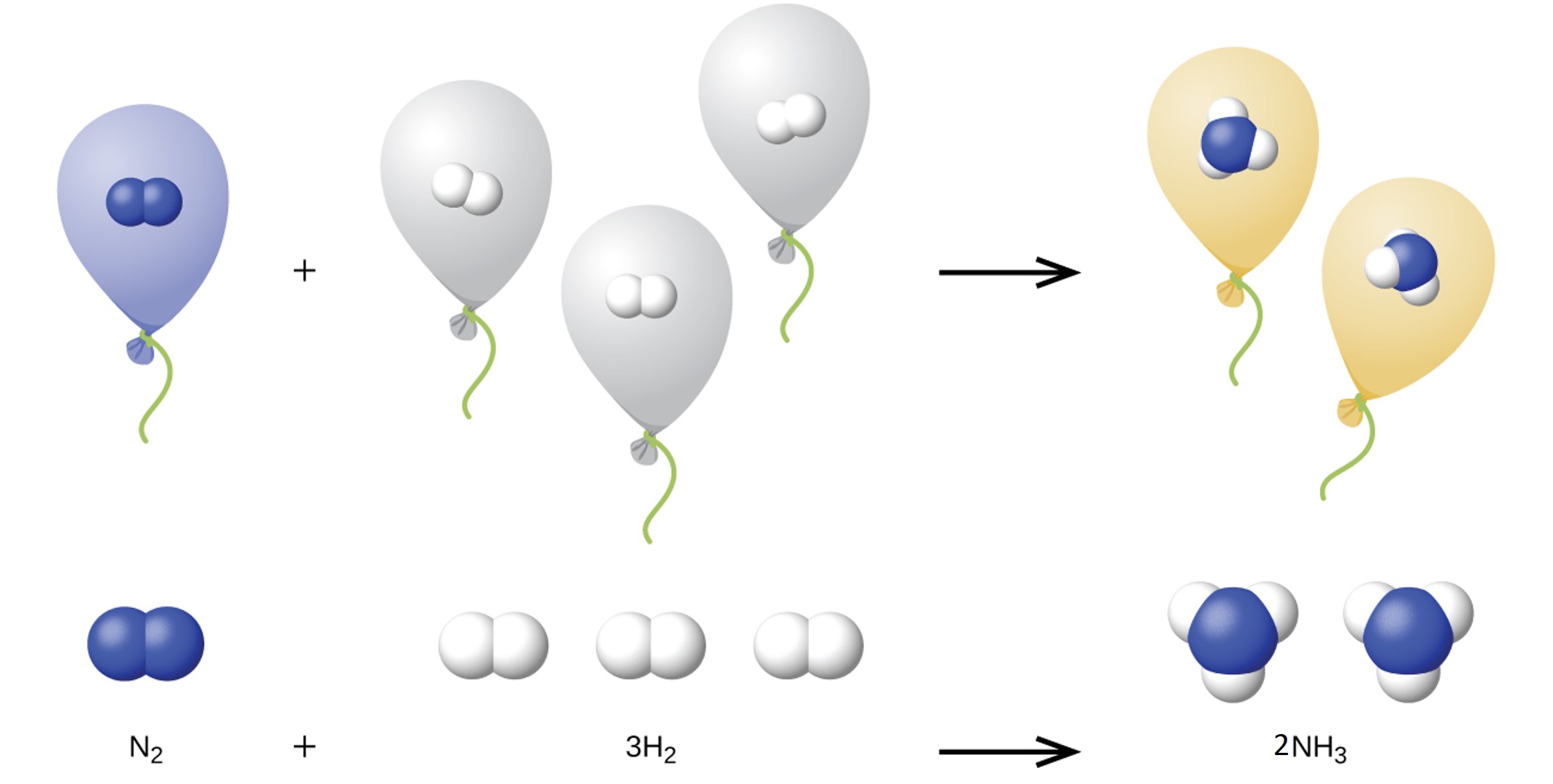
We can extend Avogadro’s law (that the volume of a gas is directly proportional to the number of moles of the gas) to chemical reactions with gases: gases combine, or react, in definite and simple proportions by volume, provided that all gas volumes are measured at the same temperature and pressure. For example, since nitrogen and hydrogen gases react to produce ammonia gas according to N2(g) + 3 H2(g)  →  2 NH3(g), a given volume of nitrogen gas reacts with three times that volume of hydrogen gas to produce two times that volume of ammonia gas, if pressure and temperature remain constant.

The explanation for this is illustrated in Figure 1. According to Avogadro’s law, equal volumes of gaseous N2, H2, and NH3, at the same temperature and pressure, contain the same number of molecules. Because one molecule of N2 reacts with three molecules of H2 to produce two molecules of NH3, the volume of H2 required is three times the volume of N2, and the volume of NH3 produced is two times the volume of N2.

This diagram provided models the chemical reaction written with formulas across the bottom of the figure. The reaction is written; N subscript 2 plus 3 H subscript 2 followed by an arrow pointing right to N H subscript 3. Just above the formulas, space-filling models are provided. Above N H subscript 2, two blue spheres are bonded. Above 3 H subscript 2, three pairs of two slightly smaller white spheres are bonded. Above N H subscript 3, two molecules are shown composed each of a central blue sphere to which three slightly smaller white spheres are bonded. Across the top of the diagram, the reaction is illustrated with balloons. To the left is a light blue balloon which is labeled “N subscript 2”. This balloon contains a single space-filling model composed of two bonded blue spheres. This balloon is followed by a plus sign, then three grey balloons which are each labeled “H subscript 2.” Each of these balloons similarly contain a single space-filling model composed of two bonded white spheres. These white spheres are slightly smaller than the blue spheres. An arrow follows which points right to two light green balloons which are each labeled “N H subscript 3.” Each light green balloon contains a space-filling model composed of a single central blue sphere to which three slightly smaller white spheres are bonded.
Figure 1. One volume of N2 combines with three volumes of H2 to form two volumes of NH3.

Example 1

Reaction of Gases
Propane, C3H8(g), is used in gas grills to provide the heat for cooking. What volume of O2(g) measured at 25 °C and 760 torr is required to react with 2.7 L of propane measured under the same conditions of temperature and pressure? Assume that the propane undergoes complete combustion.

Solution
The ratio of the volumes of C3H8 and O2 will be equal to the ratio of their coefficients in the balanced equation for the reaction:

C3H8(g) + 5 O2(g)  →  3 CO2(g) + 4 H2O(ℓ)
1 mole + 5 moles  →  3 moles + 4 moles

From the equation, we see that one volume of C3H8 will react with five volumes of O2:

2.7 L C3H8 × \dfrac{5 \;\text{L O}_2}{1 \;\rule[0.7ex]{3.5em}{0.1ex}\hspace{-3.4em}\text{L C}_3 \text{H}_8} = 13.5 L O2

A volume of 13.5 L of O2 will be required to react with 2.7 L of C3H8.

Check Your Learning
An acetylene tank for an oxyacetylene welding torch provides 9340 L of acetylene gas, C2H2, at 0 °C and 1 atm. How many tanks of oxygen, each providing 7.00 × 103 L of O2 at 0 °C and 1 atm, will be required to burn the acetylene?

2 C2H2 + 5 O2  →  4 CO2 + 2 H2O

Answer:

3.34 tanks (2.34 × 104 L)

Example 2

Volumes of Reacting Gases
Ammonia is an important fertilizer and industrial chemical. Suppose that a volume of 683 billion cubic feet of gaseous ammonia, measured at 25 °C and 1 atm, was manufactured. What volume of H2(g), measured under the same conditions, was required to prepare this amount of ammonia by reaction with N2?

N2(g) + 3 H2(g)  →  2 NH3(g)

Solution
Because equal volumes of H2 and NH3 contain equal numbers of molecules and each three molecules of H2 that react produce two molecules of NH3, the ratio of the volumes of H2 and NH3 will be equal to 3:2. Two volumes of NH3, in this case in units of billion ft3, will be formed from three volumes of H2:

683 billion ft3 NH3 × \dfrac{3\;\text{billion ft}^3 \;\text{H}_2}{2 \;\rule[0.65ex]{6.5em}{0.1ex}\hspace{-6.5em}\text{billion ft}^3 \;\text{NH}_3} = 1.02 × 103 billion ft3 H2

The manufacture of 683 billion ft3 of NH3 required 1020 billion ft3 of H2. (At 25 °C and 1 atm, this is the volume of a cube with an edge length of approximately 1.9 miles.)

Check Your Learning
What volume of O2(g) measured at 25 °C and 760 torr is required to react with 17.0 L of ethylene, C2H4(g), measured under the same conditions of temperature and pressure? The products are CO2 and water vapor.

Answer:

51.0 L

Example 3

Volume of Gaseous Product
What volume of hydrogen at 27 °C and 723 torr may be prepared by the reaction of 8.88 g of gallium with an excess of hydrochloric acid?

2 Ga(s) + 6 HCl(aq)  →  2 GaCl3(aq) + 3 H2(g)

Solution
To convert from the mass of gallium to the volume of H2(g), we need to do something like this:

This figure shows four rectangles. The first is shaded yellow and is labeled “Mass of G a.” This rectangle is followed by an arrow pointing right to a second rectangle which is shaded pink and is labeled “Moles of G a.” This rectangle is followed by an arrow pointing right to a third rectangle which is shaded pink and is labeled “Moles of H subscript 2 ( g ).” This rectangle is followed by an arrow pointing right to a fourth rectangle which is shaded lavender and is labeled “Volume of H subscript 2 ( g ).”

The first two conversions are:

8.88 g Ga × \dfrac{1 \;\rule[0.5ex]{3.3em}{0.1ex}\hspace{-3.3em}\text{mol Ga}}{69.723 \;\rule[0.5ex]{2.3em}{0.1ex}\hspace{-2.3em}\text{g Ga}} \times \dfrac{3 \;\text{mol H}_2}{2 \;\rule[0.5ex]{3.3em}{0.1ex}\hspace{-3.3em}\text{mol Ga}} = 0.191 mol H2

Finally, we can use the ideal gas law:

volume of H2 = \left(\dfrac{n\text{RT}}{\text{P}}\right)_{\text{H}_{2}} = \dfrac{0.191\;\rule[0.5ex]{1.7em}{0.1ex}\hspace{-1.7em}\text{mol}\;\times\; 0.08206 \frac{\text{L}\cdot\rule[0.3ex]{1.35em}{0.1ex}\hspace{-1.35em}\text{atm}}{\rule[0.3ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{mol}\cdot\rule[0.4ex]{0.6em}{0.1ex}\hspace{-0.6em}\text{K}}\;\times\; 300\;\rule[0.6ex]{0.8em}{0.1ex}\hspace{-0.8em}\text{K}}{0.951 \;\rule[0.5ex]{1.8em}{0.1ex}\hspace{-1.8em}\text{atm}} = 4.94 L

Check Your Learning
Sulfur dioxide is an intermediate in the preparation of sulfuric acid. What volume of SO2 at 343 °C and 1.21 atm is produced by burning l.00 kg of sulfur in oxygen?

Answer:

1.30 × 103 L

Key Concepts and Summary

The ideal gas law can be used to derive a number of convenient equations relating directly measured quantities to properties of interest for gaseous substances and mixtures. Avogadro’s law may be used in stoichiometric computations for chemical reactions involving gaseous reactants or products.

Glossary

Avogadro’s law
The volume of any ideal gas is directly proportional to the number of moles of the gas.

Chemistry End of Section Exercises

  1. Cavendish prepared hydrogen in 1766 by the novel method of passing steam through a red-hot gun barrel:
    4 H2O(g) + 3 Fe(s)  →  Fe3O4(s) + 4 H2(g)
    1. Outline the steps necessary to answer the following question: What volume of H2 at a pressure of 745 torr and a temperature of 20 °C can be prepared from the reaction of 15.0 g of H2O?
    2. Answer the question.
  2. Automobile air bags are inflated with nitrogen gas, which is formed by the decomposition of solid sodium azide (NaN3). The other product is sodium metal. Calculate the volume of nitrogen gas at 27 °C and 756 torr formed by the decomposition of 125 g of sodium azide.
  3. What volume of oxygen at 423.0 K and a pressure of 127.4 kPa is produced by the decomposition of 129.7 g of BaO2 to BaO and O2?
  4. What volume of O2 at STP is required to oxidize 8.0 L of NO at STP to NO2? What volume of NO2 is produced at STP?
  5. Ethanol, C2H5OH, is produced industrially from ethylene, C2H4, by the following sequence of reactions:
    3 C2H4 + 2 H2SO4  →  C2H5HSO4 + (C2H5)2SO4
    C2H5HSO4 + (C2H5)2SO4 + 3 H2O  →  3 C2H5OH + 2 H2SO4

    What volume of ethylene at STP is required to produce 1.000 metric ton (1000 kg) of ethanol if the overall yield of ethanol is 90.1%?

  6. Under what conditions are the ratio of stoichiometric coefficients used to balance a chemical equation the same as the volume ratio of the gaseous reactants or products? Are these conditions met when the chemical reaction takes place in a glass flask or a syringe with a moveable piston?
  7. If a syringe contains 30.0 mL of NO(g), what stoichiometric volume of O2(g) must be added to the syringe for the NO(g) and O2(g) to react and form NO2(g)?
  8. Under what conditions are the ratio of stoichiometric coefficients used to balance a chemical equation the same as the pressure ratio of the gaseous reactants or products? Are these conditions met when the chemical reaction takes place in a glass flask or a syringe with a moveable piston?
  9. If a glass flask contains 75 mmHg of O2(g), what stoichiometric pressure of NO(g) must be added to the flask for the NO(g) and O2(g) to react and form NO2(g)?
  10. A metal flask contains 3.0 mol of H2(g) and 2.0 mol of O2(g) at an initial temperature of 300. K. A spark ignites the gases and highly exothermic reaction occurs:
    2 H2(g) + O2(g)  →  2 H2O(g)

    and the temperature reaches 400. K. The initial pressure is 1.00 atm.

    1. Determine the moles of gas in the flask before and after the reaction.
    2. Determine the final pressure. Note that V remains constant.
  11. The following questions refer to the reaction:
    6 HCl(aq) + 2 Al(s)  →  2 AlCl3(aq) + 3 H2(g)
    1. Classify the chemical reaction as: a precipitation, gas-forming, oxidation-reduction, and/or combustion reaction. Select all that apply.
    2. A student combines 350.0 mL of 1.50 M HCl with excess solid Al.  Determine the volume of hydrogen gas produced.  The temperature in the laboratory is 25°C and the pressure is 0.988 atm.  Assume ideal gas behavior.
  12. Nitric acid reacts with calcium metal to produce hydrogen gas:
    2 HNO3(aq) + Ca(s)  →  Ca(NO3)2(aq) + H2(g)
    1. Classify the chemical reaction as: a precipitation, gas-forming, oxidation-reduction, and/or combustion reaction. Select all that apply.
    2. Determine the theoretical yield of hydrogen gas (in moles) if 475.0 mL of 0.500 M nitric acid reacts with excess calcium metal.
    3. The conditions in the laboratory are 725.8 torr and 23.0 °C.  Determine the theoretical yield of hydrogen gas (in liters).
    4. The scientists actually collect 2.33 L hydrogen gas.  Determine the percent yield of hydrogen gas.
  13. A chemist forms an oxide of manganese in the laboratory. In the experiment, a 4.057 g sample of solid manganese reacts with 985 mL of oxygen gas, O2, at 1.74 atm and 362 °C. After the reaction is complete, there are 1.648 g of excess manganese.
    1. How many moles of oxygen gas, O2, are consumed in the reaction?
    2. Name one assumption you had to make to use the ideal gas equation in part (a).
    3. What is the formula of the ionic compound formed between manganese and oxygen?
  14. At STP, 2.0 L of nitrogen gas fully reacts with 6.0 L of Cl2(g) to produce 4.0 L of product. What is the formula of the product?
  15. A sample of chromium metal (mass of 0.563 g) reacts with 294 mL of chlorine gas at STP.  After the reaction is complete, there are 0.108 g of excess solid.  What is the formula of the salt formed between chromium and chlorine?

Answers to Chemistry End of Section Exercises

  1. (a) First, convert grams H2O to moles of H2. Then, solve for pressure using the ideal gas law
    (b) 20.4 L H2
  2. 71.4 L
  3. 10.57 L O2
  4. 4.0 L O2; 8.0 L NO2
  5. 5.40 × 105 L
  6. When the reaction is carried out at constant pressure and temperature; a syringe with a moveable piston.
  7. 15.0 mL
  8. When the reaction is carried out at constant volume and temperature; a glass flask.
  9. 150 mmHg
  10. (a) moles of gas total before reaction: 5.0 mol; moles of gas total after reaction: 3.5 mol
    (b) 0.93 atm
  11. (a) gas-forming and oxidation-reduction; (b) 6.50 L
  12. (a) gas-forming and oxidation-reduction; (b) 0.119 mol; (c) 3.02 L; (d) 77.2% yield
  13. (a) 0.0329 mol
    (b) Particles have no volume; or Particles exert no forces on each other; or Kinetic energy is unchanged when gases collide with each other or the walls
    (c) Mn2O3
  14. NCl3
  15. CrCl3
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂
  1. “Quotations by Joseph-Louis Lagrange,” last modified February 2006, accessed February 10, 2015, link. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.