M17Q6: ΔG°, K and Van’t Hoff Plots
Learning Objectives
- Recognize that when Q < K, ΔG < 0 and a reaction proceeds to form more products until equilibrium is reached (Q = K, ΔG = 0). Recognize that when Q > K, ΔG > 0 and a reaction proceeds to form more reactants until equilibrium is reached (Q = K, ΔG = 0).
- Calculate Gibbs free energy from the reaction quotient or equilibrium constant, and vice versa.
- Prepare and/or interpret a Van’t Hoff plot to determine thermodynamic information.
| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |
For a system at equilibrium, Q = K and ΔG = 0, and the equation
ΔG = ΔG° + RT ln(Q)
may be written as
0 = ΔG° + RT ln(K) (at equilibrium)
ΔG° = –RT ln(K) or K = e-ΔG°/(RT)
This form of the equation provides a useful link between these two essential thermodynamic properties, and it can be used to derive equilibrium constants from standard free energy changes and vice versa. The relations between standard free energy changes and equilibrium constants are summarized in Table 1.
| K | ΔG° | Comments |
|---|---|---|
| > 1 | < 0 | Products are more abundant at equilibrium. |
| < 1 | > 0 | Reactants are more abundant at equilibrium. |
| = 1 | = 0 | Reactants and products are equally abundant at equilibrium. |
Example 1
Calculating an Equilibrium Constant using Standard Free Energy Change
Given that the standard free energies of formation of Ag+(aq), Cl−(aq), and AgCl(s) are 77.1 kJ/mol, −131.2 kJ/mol, and −109.8 kJ/mol, respectively, calculate the solubility product, Ksp, for AgCl. The temperature is 298 K.
Solution
The reaction of interest is the following:
AgCl(s) ⇌ Ag+(aq) + Cl–(aq) Ksp = [Ag+][Cl–]
The standard free energy change for this reaction is first computed using standard free energies of formation for its reactants and products:
ΔG° = [ΔGf°(Ag+(aq)) + ΔGf°(Cl–(aq))] – [ΔGf°(AgCl(s))]
ΔG° = [77.1 ![]() – 131.2
– 131.2 ![]() ] – [-109.8
] – [-109.8 ![]() ] = 55.7
] = 55.7 ![]()
The equilibrium constant for the reaction may then be derived from its standard free energy change:
Ksp = e-ΔG°/(RT) = e-(55.7 × 103 ![]() )/(8.314
)/(8.314 ![]() × 298.15 K) = e-22.740 = 1.74 × 10-10
× 298.15 K) = e-22.740 = 1.74 × 10-10
This result is in reasonable agreement with the value provided in Appendix J.
Check Your Learning
Use the thermodynamic data provided in Appendix F to calculate the equilibrium constant for the dissociation of dinitrogen tetroxide at 25 °C.
2 NO2(g) ⇌ N2O4(g)
Answer:
K = 6.74
From ΔG° = –RT ln K and ΔG° = ΔH° – TΔS°, we can derive a relationship between K and temperature:
–RT ln(K) = ΔH° – TΔS°
Divide both sides by –RT gives
ln(K) = –![]()
ln(K) = –![]()
This equation is known as the van’t Hoff Equation. By calculating equilibrium constants at various temperatures, the slope and y-intercept are related to ΔH° and ΔS°. Note that there is an underlying assumption that ΔH° and ΔS° of a reaction do not vary as a function of temperature. While not explicitly true, it is an assumption we will generally make in this course, unless otherwise specified.
ln(K) = –![]()
y = m x + b
Therefore, a plot of ln(K) vs. ![]() would yield a slope of –
would yield a slope of –![]() and an intercept of
and an intercept of ![]() . This is the van’t Hoff plot. By experimentally measuring the concentrations of reactants and products at various temperatures, making the van’t Hoff plot would yield the change in enthalpy and entropy of the reaction from the experimental data.
. This is the van’t Hoff plot. By experimentally measuring the concentrations of reactants and products at various temperatures, making the van’t Hoff plot would yield the change in enthalpy and entropy of the reaction from the experimental data.
For an exothermic reaction (ΔH° < 0), K decreases with increasing temperature, whereas for an endothermic reaction (ΔH° > 0), K increases with increasing temperature. This quantitative relationship here agrees with the qualitative predictions made by applying Le Chatelier’s principle. It also shows that the magnitude of ΔH° dictates how rapidly K changes as a function of temperature. In contrast, ΔS° affects the magnitude of K, but not its temperature dependence.
Example 2
Interpreting a van’t Hoff plot
Consider a plot of ln(K) vs ![]() with a slope of 327.3 K and a y-intercept of 5.91. What are the values of ΔH° and ΔS°?
with a slope of 327.3 K and a y-intercept of 5.91. What are the values of ΔH° and ΔS°?
Solution
ΔH°: The slope is equal to –![]() . Solving for ΔH°:
. Solving for ΔH°:
ΔH° = -slope × R = -(327.3 K)(8.314 ![]() ) = -2721
) = -2721 ![]() = -2.721
= -2.721 ![]()
ΔS°: The y-intercept is equal to ![]() . Solving for ΔS°:
. Solving for ΔS°:
ΔS° = y-int × R = (5.91)(8.314 ![]() ) = 49.1
) = 49.1 ![]()
Check Your Learning
Consider a plot of ln(K) vs ![]() with a slope of -296.1 K and a y-intercept of 2.54. What are the values of ΔH° and ΔS°?
with a slope of -296.1 K and a y-intercept of 2.54. What are the values of ΔH° and ΔS°?
Answer:
ΔH° = 2.462 kJ/mol; ΔS° = 21.1 J/mol·K
Key Concepts and Summary
Bringing together Gibbs Free Energy and Equilibrium, products are more abundant when K > 1 and ΔG° < 0, reactants are more abundant when K < 1 and ΔG° > 0, and reactants and products are equally abundant when K = 1 and ΔG° = 0. By measuring the equilibrium constant as temperature changes, the enthalpy and entropy of the system can be easily calculated from the slope and the y-intercept of a van’t Hoff plot.
Key Equations
- ΔG° = –RT ln(K)
- ln(K) = –
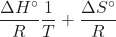
Glossary
- van’t Hoff equation
- relates the equilibrium constant (K) and temperature, with the slope related to the enthalpy and the y-intercept related to the entropy of the system
- van’t Hoff plot
- a plot of ln(K) vs
 , which yields a slope of –
, which yields a slope of –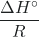 and an intercept of
and an intercept of 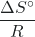
Chemistry End of Section Exercises
- Calculate ΔG° for each of the following reactions from the equilibrium constant at the temperature given:
- N2(g) + O2(g) ⇌ 2 NO(g); T = 2.0 × 103 °C; K = 4.1 × 10-4
- H2(g) + I2(g) ⇌ 2 HI(g); T = 400.0°C; K = 50.0
- CO2(g) + H2(g) ⇌ CO(g) + H2O(g); T = 980°C; K = 1.67
- Consider the process of dissolving CuS solid in water: CuS(s) ⇌ Cu2+(aq) + S2–(aq)
- Use the thermochemical data from Appendix F, to calculate ΔG° at room temperature, 298 K.
- Calculate Ksp for the reaction at 298 K.
- Use the thermochemical data from Appendix F, to calculate ΔG° at 373 K.
- Calculate Ksp at 373 K.
- Use the thermochemical data from Appendix F, calculate the equilibrium constant at the temperature given:
- C2H2(g) + H2(g) ⇌ C2H6(g); T = 298 K
- O2(g) + 2 F2(g) ⇌ 2 F2O(g); T = 100.0 °C
- I2(s) + Br2(ℓ) ⇌ 2 IBr(g); T = 0.0 °C
- 2 LiOH(s) + CO2(g) ⇌ Li2CO3(s); T = 575 °C
- Hydrogen peroxide, H2O2, decomposes according to the equation:
H2O2(ℓ) → H2O(ℓ) + ½ O2(g) ΔrH° = -98.2 kJ/mol, ΔrS° = 70.1 J/mol∙K
Calculate equilibrium constant for this reaction at 25 °C.
- At room temperature, the equilibrium constant (Kw) for the self-ionization of water is 1.00 × 10−14. Using this information, calculate the standard free energy change for the aqueous reaction of hydrogen ion with hydroxide ion to produce water. (Hint: The reaction is the reverse of the self-ionization reaction.)
- Consider the decomposition of CaCO3(s) into CaO(s) and CO2(g). What is the equilibrium partial pressure of CO2 at room temperature? The thermochemical data from Appendix F will prove useful.
- The equilibrium constant for the reaction: AgBr(s) ⇌ Ag+(aq) + Br–(aq), is Ksp = 7.7 × 10-13 at 25 °C. Calculate ΔG for the reaction when [Ag+] = 1.0 × 10-2 M and [Br–] = 1.0 × 10-3 M. Is this reaction spontaneous or nonspontaneous at these concentrations?
- A plot of ln(K) vs
 for the reaction of hydrogen gas and carbon dioxide to produce water and carbon monoxide has a slope of -4.96 × 103 K and a y-intercept of 5.06. What is ΔH°, ΔS°, ΔG° and K at 298 K?
for the reaction of hydrogen gas and carbon dioxide to produce water and carbon monoxide has a slope of -4.96 × 103 K and a y-intercept of 5.06. What is ΔH°, ΔS°, ΔG° and K at 298 K? - The following plot of ln(K) vs
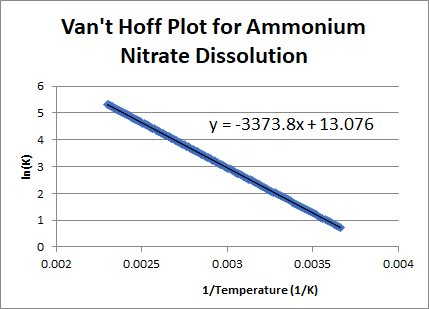
 was created for the process of dissolving ammonium nitrate. From this, calculate ΔH°, ΔS°, ΔG° and K at 298 K.
was created for the process of dissolving ammonium nitrate. From this, calculate ΔH°, ΔS°, ΔG° and K at 298 K.
- The van’t Hoff plot for the reaction: 2 SO2(g) + O2(g) ⇌ 2 SO3(g), is shown below.
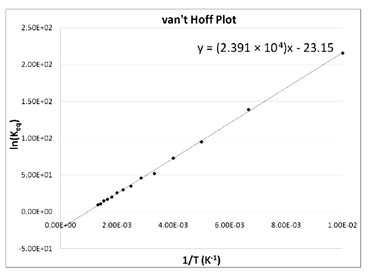
- What is the standard enthalpy, ΔH°, for this reaction?
- What is the standard entropy, ΔS°, for this reaction?
- What is the standard Gibbs Free Energy, ΔG°, for this reaction at 298 K?
Answers to Chemistry End of Section Exercises
- (a) 1.5 × 102 kJ/mol; (b) -21.9 kJ/mol; (c) -5.34 kJ/mol
- (a) ΔG° = 204.9 kJ/mol at 298 K (Note that ions do not have ΔG° = 0 at 298 K)
(b) Ksp = 1.22 × 10-36
(c) ΔG° = 208.4 kJ/mol at 373 K (Note that you must first find ΔH° = 140.97 kJ/mol and ΔS° = -180.7 J/mol·K, and then use ΔG = ΔH – TΔS to find ΔG° at the higher temperature)
(d) Ksp = 6.589 × 10-30 - (a) ΔG° = -241.02 kJ/mol; K = 2.653 × 1042
(b) ΔG° = 92.6 kJ/mol; K = 1.08 × 10-13
(c) ΔG° = 13.6; K = 2.49 × 10-3
(d) ΔG° = 324.7 kJ/mol; K = 1.00 × 10-20 - K = 7.5 × 1020
- 79.9 kJ/mol
- PCO2 = 1.42 × 10-23 atm
- ΔG = 41 kJ/mol, nonspontaneous
- ΔH° = 41.2 kJ/mol; ΔS° = 42.1 J/mol·K; ΔG° = 28.7 kJ/mol; K = 9.314 × 10-6
- ΔH° = 28.05 kJ/mol; ΔS° = 108.7 J/mol·K; ΔG° = -4.34 kJ/mol; K = 5.78
- (a) ΔH° = -198.7 kJ/mol: (b) ΔS° = -192.5 J/mol·K; (c) ΔG° = -141.3 kJ/mol
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

