M7Q8: Core and Valence Electrons, Shielding, Zeff
Introduction
This section continues to explore the relationship between an atom’s electron arrangement in orbitals and the chemical properties of that atom. As we move from hydrogen to multi-electron atoms there is an incredible increase in complexity due to the fact that electrons repel each other. Nonetheless, one can still understand much of the periodic table and the trends in properties of atoms and ions by using approximations that are based on using the quantum numbers of individual electrons in an atom. These properties vary periodically as the electronic structure of the elements changes.
Learning Objectives for Core and Valence Electrons, Shielding, Zeff
- Distinguish between core and valence electrons.
| Core and Valence Electrons | - Correlate the effective nuclear charge with selected trends in periodic properties.
| Effective Nuclear Charge (Zeff) | Shielding |
| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |
Core and Valence Electrons
The electrons occupying the outermost shell orbital(s) are called valence electrons, and those occupying the inner shell orbitals are called core electrons (Figure 1). They can be more easily distinguished when using the noble gas configuration. For some examples, let us consider the ground state electron configurations of the elements in the 3rd period of the periodic table. For sodium, [Ne]3s1, the symbol [Ne] represents core electrons (1s22s22p6) and the valence electron is the electron in the 3s orbital.
![This figure includes the element symbol N a, followed by the electron configuration for the element. The first part of the electron configuration, 1 s superscript 2 2 s superscript 2 2 p superscript 6, is shaded in purple and is labeled, “core electrons.” The last portion, 3 s superscript 1, is shaded orange and is labeled, “valence electron.” To the right of this configuration is the word “Abbreviation” followed by [ N e ] 3 s superscript 1.](https://wisc.pb.unizin.org/app/uploads/sites/557/2019/05/CNX_Chem_06_04_Valence.jpg)
Compare this to the abbreviated configuration of lithium, [He]2s1, where [He] represents the configuration of the helium atom, which is identical to that of the filled inner shell of lithium. And the abbreviated configuration of potassium, [Ar]4s1, where [Ar] represents the configuration of the argon atom, which is identical to that of the filled inner shell of potassium.
Writing the configurations in this way emphasizes the similarity of the configurations of lithium, sodium and potassium. All three atoms, which are in the alkali metal family, have only one electron in a valence s subshell outside a filled set of inner shells.
Li: [He]2s1
Na: [Ne]3s1
K: [Ar]4s1
The alkaline earth metal magnesium with its 12 electrons in a [Ne]3s2 configuration, is analogous to its family members beryllium, [He]2s2, and calcium, [Ar]4s2. All three atoms have a filled s subshell outside their filled inner shells.
Aluminum (atomic number 13), with 13 electrons and the electron configuration [Ne]3s23p1, is analogous to its family member boron, [He]2s22p1. The electron configurations of silicon (14 electrons), phosphorus (15 electrons), sulfur (16 electrons), chlorine (17 electrons), and argon (18 electrons) are analogous in the electron configurations of their outer shells to their corresponding family members carbon, nitrogen, oxygen, fluorine, and neon, respectively, except that the principal quantum number of the outer shell of the heavier elements has increased by one to n = 3. Figure 2 shows the ground-state electron configuration for the outer-shell electrons of these elements as well as that for atoms of each of the known elements. (note that for p-block elements in periods 4-7, the outer-shell configurations in Figure 2 includes more than just the valence electrons; it also shows the full d and f subshells for clarity.)
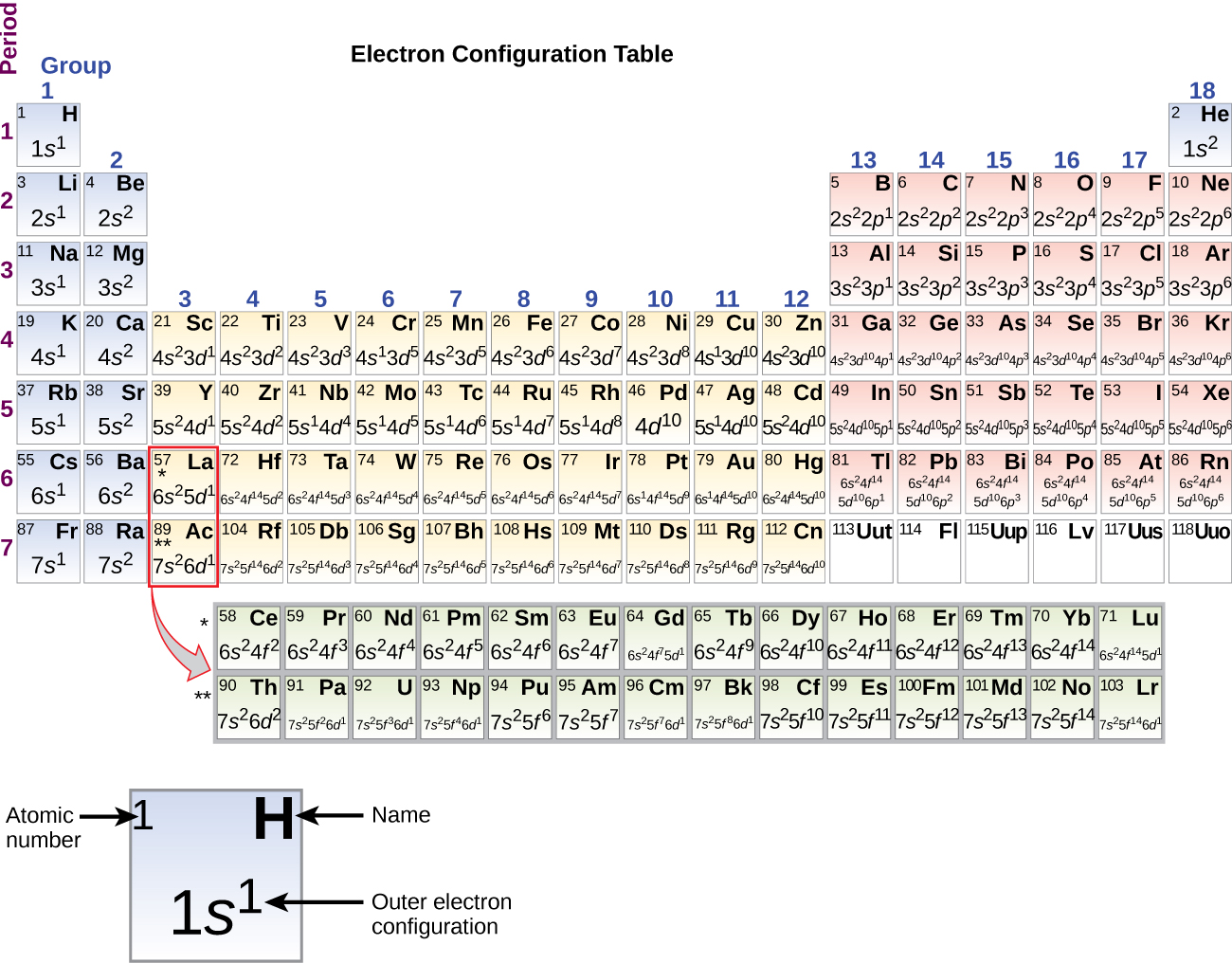
Effective Nuclear Charge (Zeff)
For an atom or an ion with only a single electron, we can calculate the potential energy of an electron by considering only the electrostatic attraction between the positively charged nucleus and the negatively charged electron. When more than one electron is present, however, the total energy of the atom or the ion depends not only on attractive electron-nucleus interactions but also on repulsive electron-electron interactions. For example, in helium there are two electrons. From Coloumb’s law we know that there is a repulsive interaction that depends on the distance between them. In addition there are attractive interactions between each of the two electrons with the nucleus. There are no known solutions to the Schrodinger equation for this problem, so one must use approximate methods to find the orbitals and their energies.
If an electron is far from the nucleus (i.e., if the distance r between the nucleus and the electron is large), then at any given moment, most of the other electrons will be between that electron and the nucleus. Hence these electrons will cancel a portion of the positive charge of the nucleus and thereby decrease the attractive interaction between the nucleus and the electron farther away. As a result, the electron farther away experiences an effective nuclear charge (Zeff). An effective nuclear charge is the nuclear charge an electron actually experiences because of shielding from other electrons closer to the nucleus (Figure 3). Consequently, the Zeff is always less than the actual nuclear charge, Z. The Zeff experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present.
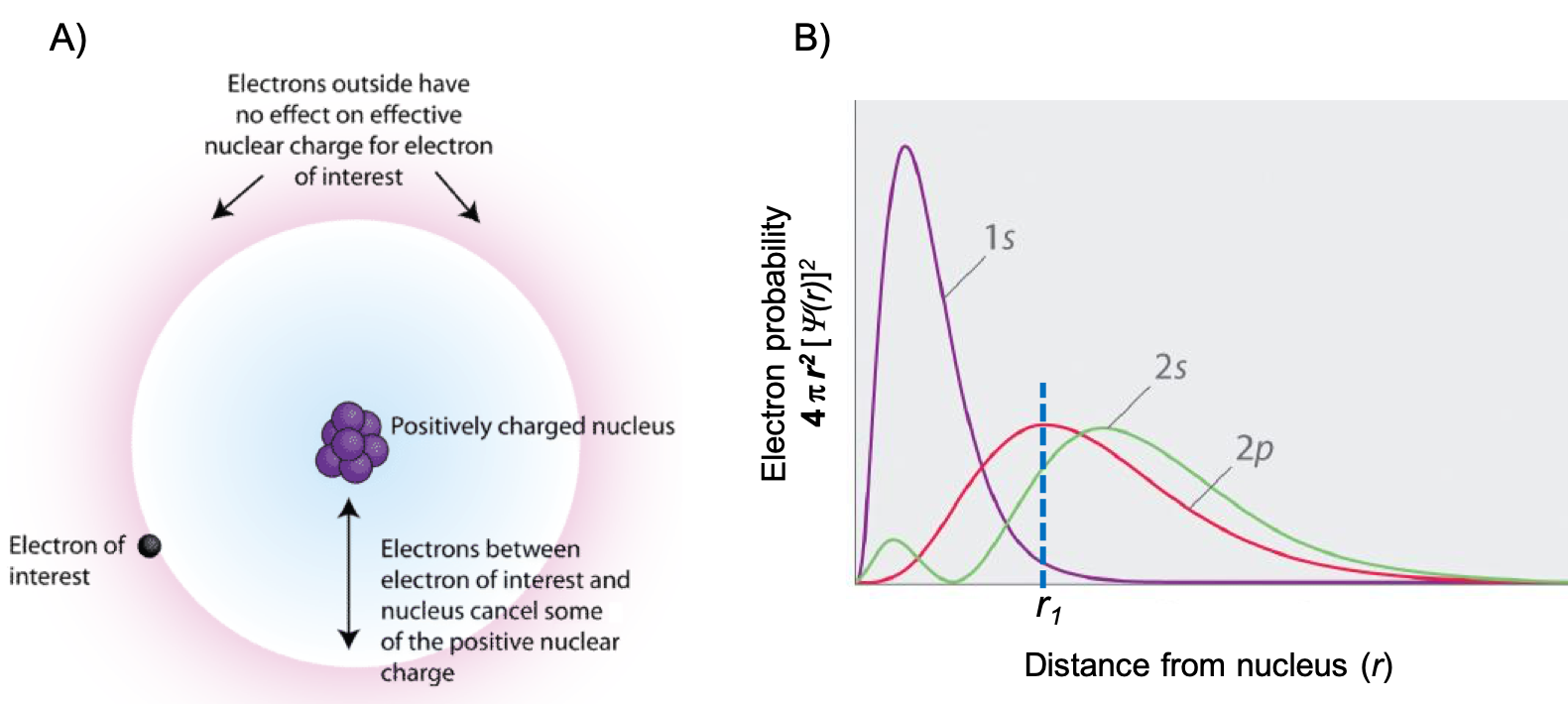
Shielding is determined by the probability of another electron being between the electron of interest and the nucleus, as well as by the electron–electron repulsions the electron of interest encounters. Core electrons are adept at shielding, while electrons in the same valence shell do not block the nuclear attraction experienced by each other as efficiently. In Figure 3B, if a 2p electron exists at a distance r1, most likely the 1s electrons (core electrons) will be between the electron of interest and the nucleus. But, there is only a small probability of the 2s electron (electron in the same valence shell) to shield the 2p electron of interest. Thus, each time we move from one element to the next across a period, Z increases by one, but the shielding increases only slightly. Thus, Zeff for valence electrons increases as we move from left to right across a period. In this class, we will calculate Zeff = Z – S, where S is the number of core electrons that are shielding the valence electrons. There are more exact ways of determining Zeff which include the shielding contribution of electrons in the same shell, but the approximate formula we use in this course is accurate enough to be very useful. Remember from a previous chapter, Z is the number of protons in the nucleus. Note that while we often refer to the Zeff of a valence electron, we can calculate the Zeff for any electron by taking into account only the number of core electrons that are shielding. For example, consider a 2s electron of Cl. For Cl, Z = 17 and the electron configuration is 1s22s22p63s23p5. The only electrons that will shield a 2s electron are the 1s electrons, and there are two of them. Therefore, Zeff = 17 – 2 = 15 for a 2s electron of Cl. The Zeff for a 3p electron, on the other hand, is Zeff = 17 – 10 = 7 because there are 10 electrons shielding the 3p electron (2 electrons in n = 1 and a total of 8 electrons in n = 2).
Key Concepts and Summary
Electrons in the outermost orbitals are called valence electrons. In the periodic table, elements with analogous valence electron configurations usually occur within the same group (column). There are some exceptions to the predicted filling order, particularly when half-filled or completely filled orbitals can be formed. The periodic table can be divided into three categories based on the orbital in which the last electron to be added is placed: main group elements (s and p orbitals), transition elements (d orbitals), and inner transition elements (f orbitals).
Effective nuclear charge is the nuclear charge an electron actually experiences. The Zeff experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present. For valence electrons, Zeff increases from left to right across a period and decreases down a group.
Key Equations
- Zeff = Z – S, where S is the number of core electrons
Glossary
- core electrons
- electrons occupying the inner shell orbitals
- effective nuclear charge
- charge that leads to the Coulomb force exerted by the nucleus on an electron, calculated as the nuclear charge minus shielding
- valence electrons
- electrons in the outermost or valence shell (highest value of n) of a ground-state atom; determine how an element reacts
- valence shell
- outermost shell of electrons in a ground-state atom; for main group elements, the orbitals with the highest n level (s and p subshells) are in the valence shell, while for transition metals, the highest energy s and d subshells make up the valence shell and for inner transition elements, the highest s, d, and f subshells are included
Chemistry End of Section Exercises
- Which of the following atoms contains only three valence electrons: Li, B, N, F, Ne?
- Identify the number of core and valence electrons for Cu and Si.
- Atoms of which group in the periodic table have a valence shell electron configuration of ns2np3?
- Atoms of which group in the periodic table have a valence shell electron configuration of ns2?
- Use an orbital diagram to describe the electron configuration of the valence shell of each of the following atoms:
- N
- Si
- Fe
- Te
- Mo
- Select the atom in which valence electron(s) experience the greatest effective nuclear charge (Zeffective).
- Potassium
- Calcium
- Selenium
- Bromine
- They are all the same.
Answers to Chemistry End of Section Exercises
- B
- Cu: 18 core electrons and 11 valence electrons
Si: 10 core electrons and 4 valence electrons - 15 (5A)
- 2 (2A)
- (a)

(b)
(c)
(d)
(e)
- D
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

