M7Q4: Wave Interference, Diffraction

Introduction

As the quest continued to resolve scientific paradoxes in classical physics, scientists needed to completely revise the way they thought about matter. This section examines the behavior of interference and diffraction of waves.

Learning Objectives for Wave Interference, Diffraction

| Key Concepts and Summary | Glossary |

Wave Interference and Diffraction

If you were to drop a stone into a still pond, you would see waves ripple outward from the center of a circle. If you were to drop multiple stones into a still pond, you would see these same waves ripple outward, but when the waves meet, the pattern would change. When two or more waves come into contact, they interfere with each other. Interacting waves on the surface of water can produce interference patterns similar to those shown below (Figure 1).

A photograph is shown of ripples in water. The ripples display an interference pattern with each other.
Figure 1. An interference pattern on the water surface is formed by interacting waves. The waves are caused by the disturbance of water by the rocks. (credit: modification of work by Sukanto Debnath)

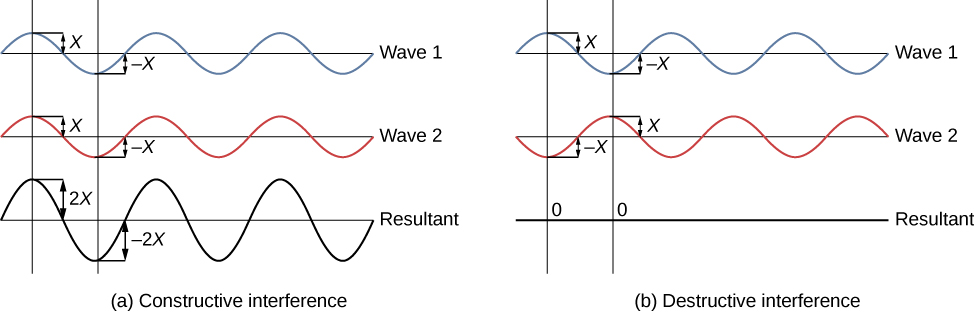
There are two types of wave interference. Constructive interference occurs in regions where the peaks or troughs for the two waves coincide (Figure 2a). Destructive interference occurs in regions where the peak of one wave coincides with the trough of another wave (Figure 2b). The amplitudes of the interfering waves add together and produce a resultant wave, as shown below.

This image has two parts. On the left side (part A), there are three horizontal lines. Wave 1 is plotted on the top line, Wave 2 is plotted on the middle line, and the Resultant wave is plotted on the bottom line. Waves 1 and 2 are aligned so that the peaks and troughs line up perfectly. The amplitude of Wave 1 is labeled as "x" and the amplitude of Wave 2 is labeled as "x". The resultant wave has an amplitude labeled as "2x" because the amplitudes add together. On the right side of the figure (part B), there are the same three horizontal lines with waves labeled "Wave 1", "Wave 2" and "Resultant". In this part, however, the peak of Wave 1 (with amplitude "x") is aligned with the trough of Wave 2 (with amplitude "-x"). The resultant wave therefore has an amplitude of 0 when the waves are added together.
Figure 2. The amplitudes of waves add. (a) Pure constructive interference is obtained when identical waves are in phase. (b) Pure destructive interference occurs when identical waves are exactly out of phase, or shifted by half a wavelength.

Diffraction of waves occurs when a wave encounters an obstacle—the wave appears to bend around a small obstacle or spread out in semicircles after an opening. Consider the water waves in Figure 3 that show how water waves diffract and form large semicircles after passing through a breakwater.

Waves approaching the beach from the ocean that pass through a breakwater form semicircular waves.
Figure 3. Waves pass through a breakwater in Ashkelon, Israel and form a semicircular pattern. (credit: “Dmitris1″/Wikimedia Commons CC BY-SA 4.0)

Light Behaves as a Wave

The interference that is seen in water waves is also seen with light, which indicates that light behaves like a wave. Figure 4 shows the interference patterns that arise when light passes through narrow slits closely spaced about a wavelength apart. If light behaved as a classic particle, shining a light through two narrowly spaced slits would result in just two lines on the screen (one for the light particles passing through each slit). The fact that an interference pattern occurs indicates that a pure particle definition of light is not accurate. The fringe patterns produced depend on the wavelength. If you were to pass short and long wavelength light through a set of slits, the shorter wavelength light will produce more closely spaced fringes than longer wavelength light. When the light passes through the two slits, each slit effectively acts as a new source, resulting in two closely spaced waves coming into contact at the detector (the camera in this case). The dark regions in Figure 4 correspond to regions where the peaks for the wave from one slit happen to coincide with the troughs for the wave from the other slit (destructive interference), while the brightest regions correspond to the regions where the peaks for the two waves (or their two troughs) happen to coincide (constructive interference). Such interference patterns cannot be explained by particles moving according to the laws of classical mechanics.

This image shows interference patterns for light passing through a narrow slit. Four distinct colored bands are arranged from top to bottom. The top band shows white light, the second red, the third green, and the fourth is blue. Each band shows a central square of color with narrower vertically oriented bands extending left and right on a black background.
Figure 4. Interference fringe patterns are shown for light passing through two closely spaced, narrow slits. The spacing of the fringes depends on the wavelength, with the fringes being more closely spaced for the shorter-wavelength blue light. (credit: PASCO)

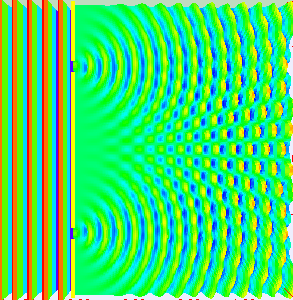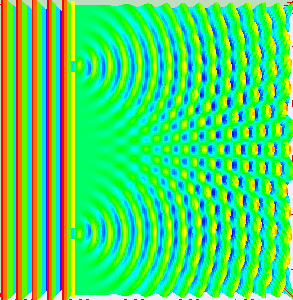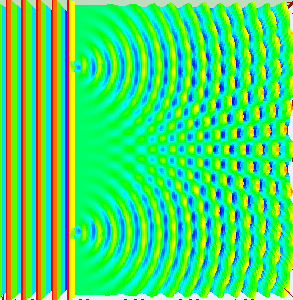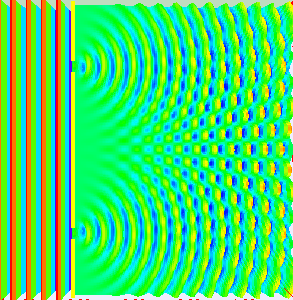
If light passes through a slit, it will also produce a similar wave pattern as depicted in Figure 3. A wave passing through two small openings spaced closely together will spread out and begin to interfere, as seen in Figure 5. A wave comes from the left and is incident on two slits, which diffract the plane wave. The interference pattern produced when light diffracts cannot be explained by particles moving according to the laws of classical mechanics and will be discussed in greater detail in the following section.

A simulation of a plane wave being diffracted through two slits is shown from an aerial perspective. Imagine a wave in the middle of the ocean that is moving in a straight line without any disturbances. From an aerial perspective in this simulation, we see the peaks as red and the troughs as blue. So the simulation shows these lines as alternating. When the plane wave passes through two small slits, diffraction occurs as the plane wave forms semicircular patterns on the other side of the slit. The semicircular pattern forms at each slit. When the semicircles from each slit meet, they exhibit interference. On the far right side of the frame, we see that as the waves hit the boundary of the gif, there are parts where there is no color because the waves have canceled each other out.
Figure 5. A plane wave coming from the left passes through two slits and produces an interference pattern.

Since the photoelectric effect showed that light has particle-like characteristics, and light diffraction and interferences shows that light has wave-like properties, we often refer to the wave-particle duality of light: Light has both wave-like and particle-like properties.

Key Concepts and Summary

Waves exhibit diffraction and interference. Electromagnetic radiation that passes through two closely spaced narrow slits having dimensions roughly similar to the wavelength will show an interference pattern that is a result of constructive and destructive interference of the waves. Since light is diffracted when passing through narrow slits, and since light can produce interference patterns, we say that light behaves as a wave. These processes cannot be explained by particles moving according to classical mechanics.

Glossary

constructive interference
when the peaks or troughs for two waves coincide to produce a wave that is the sum of the two individual waves
destructive interference
when the peak of one wave coincides with trough of another wave to either cancel the wave entirely or produce a smaller wave
diffraction
the process by which a beam of light is spread out upon encountering an obstacle in its path, typically accompanied by interference between the wave forms produced

Chemistry End of Section Exercises

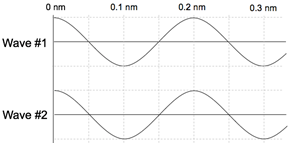
  1. True or False: The following waves would interfere constructively.
    Figure shows two waves. Wave 1 has maximum at 0 nm and 0.2 nm, and minimum at 0.1 nm and 0.3 nm. Wave 2 has maximum at 0 nm and 0.2 nm, and minimum at 0.1 nm and 0.3 nm.

Answers to Chemistry End of Section Exercises

  1. True
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.