D31.4 Arrhenius Equation and Arrhenius Plot
The relationship between the activation energy, temperature, steric factor and the rate constant for a given reaction is summarized by the Arrhenius equation:
The constant A is called the frequency factor and it depends on the rate at which collisions occur and the fraction of collisions that have the correct orientation (steric factor). The exponential term, e-Ea/RT, is the fraction of the total number of collisions that has sufficient energy to overcome the activation-energy barrier of the reaction.
The Arrhenius equation describes quantitatively much of what we have already discussed about reaction rates. For example, for two similar reactions occurring at the same temperature, the reaction with the higher Ea has the smaller rate constant (k). Also, a change in conditions that increases the number of collisions with a favorable orientation results in an increase in A and, consequently, an increase in k.
Exercise: Calculating Rate Constants
If we take the natural logarithm of both sides of the Arrhenius equation, we have:
which has a standard linear equation format:
![Rendered by QuickLaTeX.com \begin{array}{rcccl} \text{ln}(k) & = & \left(-\dfrac{E_a}{R}\right)\left(\dfrac{1}{T}\right) &+& \text{ln}(A) \\[0.5em] y &=& m\ \ \ \ x &+& b \end{array}](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-71d6d1649b256bf4e1bdf0aa6b8c6fff_l3.png)
This provides a convenient way to experimentally determine Ea for a reaction. By measuring k at different temperatures and plotting ln(k) versus 1/T, we can obtain a straight line where slope = –Ea/R.
Activity: Determining Ea
You can estimate the activation energy without constructing an Arrhenius plot if the rate constant was determined at only two temperatures.
The slope of an Arrhenius plot is:
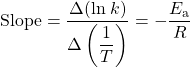
Therefore:
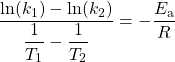
which can be rearranged as:
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

