D38.2 Enzyme Kinetics: Michaelis-Menten Mechanism

John Moore; Jia Zhou; Etienne Garand

D38.2 Enzyme Kinetics: Michaelis-Menten Mechanism

The Michaelis-Menten mechanism is a two-step reaction mechanism that applies to many enzyme-catalyzed reactions. An enzyme (E) binds with a substrate (S) to form an enzyme-substrate complex (ES), which then separates to give the product (P) and regenerates the enzyme. The overall reaction is:

S ⟶ P

with the simple two-step mechanism where the second step is rate determining:

step 1: (fast)	E + S	$\xrightleftharpoons[k_{-1}]{k_1}$	ES
step 2: (slow)	ES	$\overset{k_2}{\longrightarrow}$	P + E

The rate of the catalyzed reaction is equal to the rate of product formation:

$rate = \dfrac{\Delta[P]}{\Delta t} = k_2[ES]$

but ES is a reactive intermediate whose concentration cannot be easily measured. We need to express the reaction rate in terms of concentrations that are easily measurable. This can be done by assuming that, once the reactive intermediate, ES, forms, its concentration remains approximately constant throughout the course of the reaction; this is called the steady-state approximation. It differs from the equilibrium approximation we discussed earlier in that it is not necessary to assume step 1 has reached equilibrium. The steady-state approximation is reasonable, because once ES builds up sufficient concentration, the reactions that consume ES become faster and prevent the concentration from increasing further.

When the concentration of the enzyme-substrate complex reaches a steady state:

$\dfrac{d[ES]}{dt} = 0$

The ES complex is formed by the forward reaction in step 1, and is reacted away in the reverse reaction of step 1 and forward reaction of step 2. Summing the rates of these reactions gives:

$\dfrac{d[ES]}{dt} = k_1[E][S] - k_{-1}[ES] - k_2[ES] = 0$

Rearranging the equation to solve for [ES] gives:

$\begin{array}{rcl} (k_{-1} + k_2)[ES] &=& k_1[E][S] \\[1em] [ES] &=& \dfrac{k_1[E][S]}{k_{-1} + k_2} \end{array}$

or:

$[ES] = \dfrac{[E][S]}{K_M}$

where K_M is the Michaelis constant:

$K_M=\dfrac{k_{-1}+k_2}{k_1}$

It is difficult to know the exact concentration of the free enzyme ([E]) at any given moment. However, we do know the total concentration of enzyme, [E]_total (the enzyme must be either in its unreacted form (E) or combined with substrate (ES)):

[E]_total = [E] + [ES]

Substituting into the above equation gives:

$[ES] = \dfrac{([E]_{\text{total}} - [ES])[S]}{K_M}$

Rearranging the variables gives:

$\begin{array}{rcl} [ES] &=& \dfrac{[E]_{\text{total}}[S]}{K_M} - \dfrac{[ES][S]}{K_M} \\[1.5em] \dfrac{[ES][S]}{K_M} + [ES] &=& \dfrac{[E]_{\text{total}}[S]}{K_M} \\[1.5em] \left(\dfrac{[S] + K_M}{K_M}\right)[ES] &=& \dfrac{[E]_{\text{total}}[S]}{K_M} \\[1.5em] [ES] &=& \left(\dfrac{[E]_{\text{total}}[S]}{K_M}\right)\left(\dfrac{K_M}{[S] + K_M}\right) = \dfrac{[E]_{\text{total}}[S]}{[S] + K_M} \end{array}$

Substituting this [ES] expression into the expression for the reaction rate gives:

$\text{rate} = \dfrac{\Delta[P]}{\Delta t} = \dfrac{k_2[E]_{\text{total}}[S]}{[S]+K_M}$

or

$\text{rate} = \dfrac{V_{\text{max}}[S]}{[S]+K_M}$

This is the Michaelis-Menten equation, where V_max = k₂[E]_total is the maximum rate the reaction can achieve.

There are two limiting cases for this equation, depending on the relative values of [S] and K_M. If there are a lot of substrate, that is [S] ≫ K_M, then [S] + K_M ≈ [S]. In this case the Michaelis-Menten equation becomes:

$\text{rate} \approx \dfrac{V_{\text{max}}[S]}{[S]} = V_{\text{max}}=k_2[E]_{\text{total}}$

In other words, the reaction reaches its maximum rate, rate = V_max. In this situation, the reaction rate depends only on [E]_total and is independent of [S]. This happens when almost all of the enzyme molecules have a substrate molecule in the active site, therefore increasing the concentration of substrate can no longer increase the concentration of enzyme-substrate complex (and thus can no longer increase the rate).

On the other extreme, if there is a very small concentration of substrate, [S]≪K_M, we have [S] + K_M ≈ K_M, and the Michaelis-Menten equation becomes first-order with respect to [S]:

$\text{rate} = \left(\dfrac{V_{\text{max}}}{K_M}\right)[S]$

These two limiting cases are at the two ends of the reaction rate vs. [S] plot, as shown below.

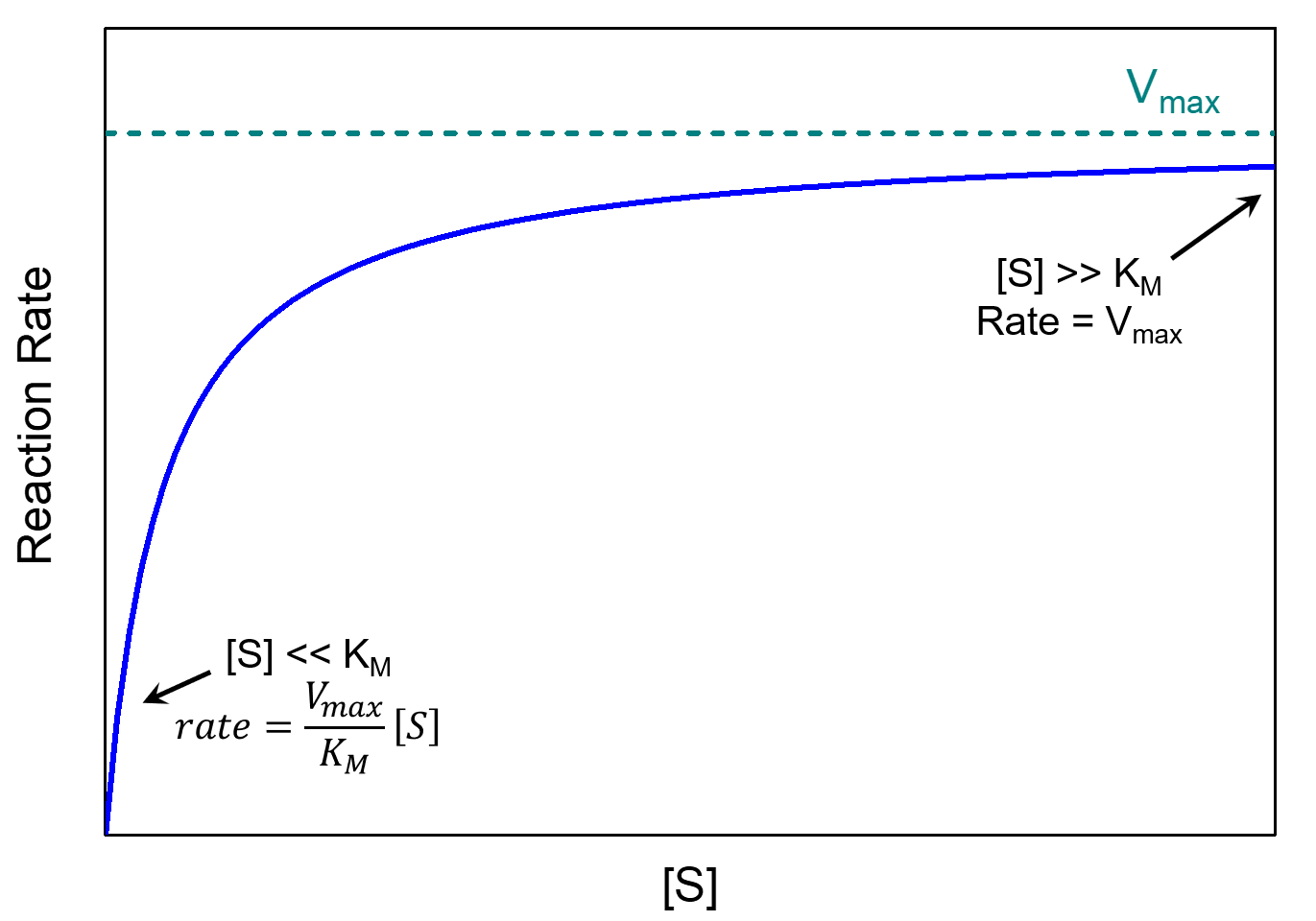
**Figure: Reaction rate as a function of substrate concentration**. At low [S], the reaction rate is first-order in [S]. As [S] increases, the rate approaches V_max.

The Michaelis constant is an inverse measure of the substrate’s affinity for the enzyme—a small K_M indicates high affinity, meaning that the rate approaches V_max more quickly. The value of K_M depends on both the enzyme and the substrate, as well as reaction conditions such as temperature and pH.

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry 109 Fall 2021 Copyright © by John Moore; Jia Zhou; and Etienne Garand is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.