D40.4 Using Standard Half-Cell Potentials
Based on the methods described in the preceding section, standard half-cell potentials have been determined for many half-cells. The table below gives half-cell potentials for selected half-cells. Click on the table to open a version that can be enlarged or printed.
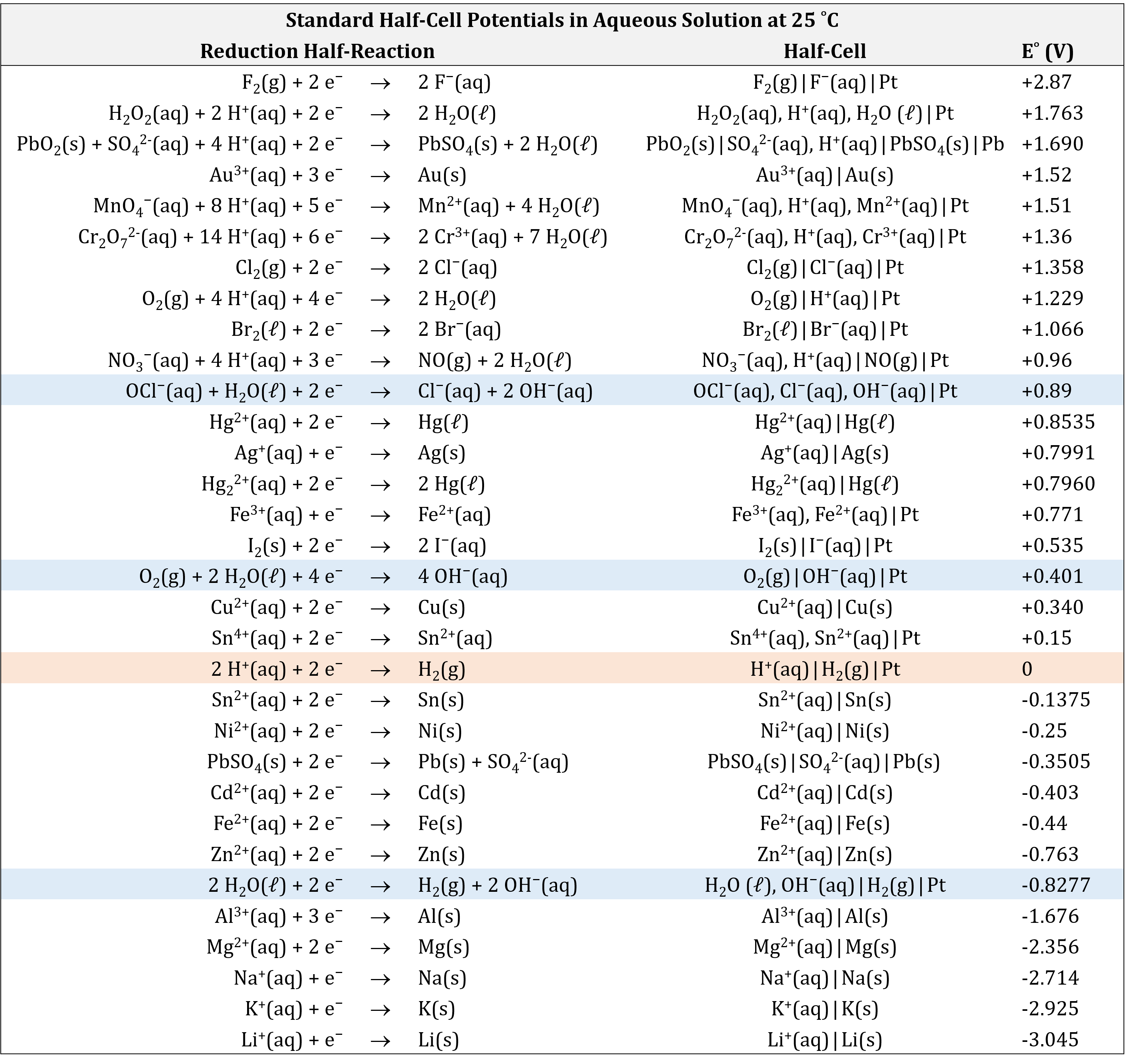
There are several important aspects to note:
- The oxidizing agent is on the reactant side of a reduction half-reaction equation.
- The strongest oxidizing agents (the substances most easily reduced) have the largest positive E° values and are at the top of the table. (For example, F2(g) is a very strong oxidizing agent.)
- The reducing agent is on the product side of a reduction half-reaction equation.
- The strongest reducing agents (the substances most easily oxidized) have the most negative E° values and are at the bottom of the table. (For example, Li(s) and K(s) are very strong reducing agents.)
- A redox reaction is product-favored when a stronger oxidizing agent reacts with a stronger reducing agent. This results in a positive value for E°cell when the oxidation half-reaction is combined with the reduction half-reaction.
- Half-cell reactions are reversible and the direction a half-cell reaction goes depends on the potential of the other half-cell to which it is connected in a cell.
The table of standard half-cell potentials can be used to determine the E°cell for any voltaic cell and predict whether a specific redox reaction is product-favored. For example, for the cell:
Because the value of E°cell is positive, the redox reaction corresponding to this cell notation is product-favored and the voltaic cell can produce electrical energy. The overall reaction can be obtained from the cell notation by writing the oxidation and the reduction half-reactions, multiplying each half-reaction by an appropriate number to balance electrons, and summing the two half-reactions:
| Oxidation (left): | Cu(s) | ⟶ | Cu2+(aq) + 2e− | E°anode = +0.340 V |
| Reduction (right): | 2 × (Ag+(aq) + e− | ⟶ | Ag(s)) | E°cathode = +0.7991 V |
| Overall: | Cu(s) + 2Ag+(aq) | ⟶ | Cu2+(aq) + 2Ag(s) | E°cell = +0.459 V |
Note that:
- Even though the reduction half-reaction is multiplied by 2, the E°cathode is not multiplied by 2 when E°cell is calculated. This is because electrical potential is a ratio of energy per coulomb of charge transferred (V = J/C). If the half-reaction is doubled, both energy and charge transferred are doubled, leaving the ratio constant.
- The oxidation half-reaction is the reverse of the reaction as shown in the half-cell potential table, but E°anode is not multiplied by -1 . This “-1” is accounted for by the fact that E°anode is subtracted from E°cathode. (In this way, the cell potential does not depend on the direction of a half-reaction; it depends only on the composition of the half-cell.)
E° for many half-cells are included in the appendix. Tables like these make it possible to determine the E°cell for many redox reactions. Moreover, by comparing the standard potentials, we can discern which species is easier to reduce/harder to oxidize/a stronger oxidizing agent (higher/more positive E°) and which species is easier to oxidize/harder to reduce/a stronger reducing agent (lower/more negative E°).
Exercise: Using Standard Half-cell Potentials
Exercise: Predicting whether a Redox Reaction is Product-favored
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

