D23.2 Le Châtelier’s Principle: Change in Concentration

For a chemical system at equilibrium at constant temperature, if the concentration of a reactant or a product is changed, therefore changing Q, the system is no longer at equilibrium because Q ≠ K. The concentrations of all reaction species will then undergo additional changes until the system reaches a new equilibrium with a different set of equilibrium concentrations. We say that the equilibrium shifts in a direction (forward or reverse) that partially counteracts the change.

For example, consider the chemical reaction:

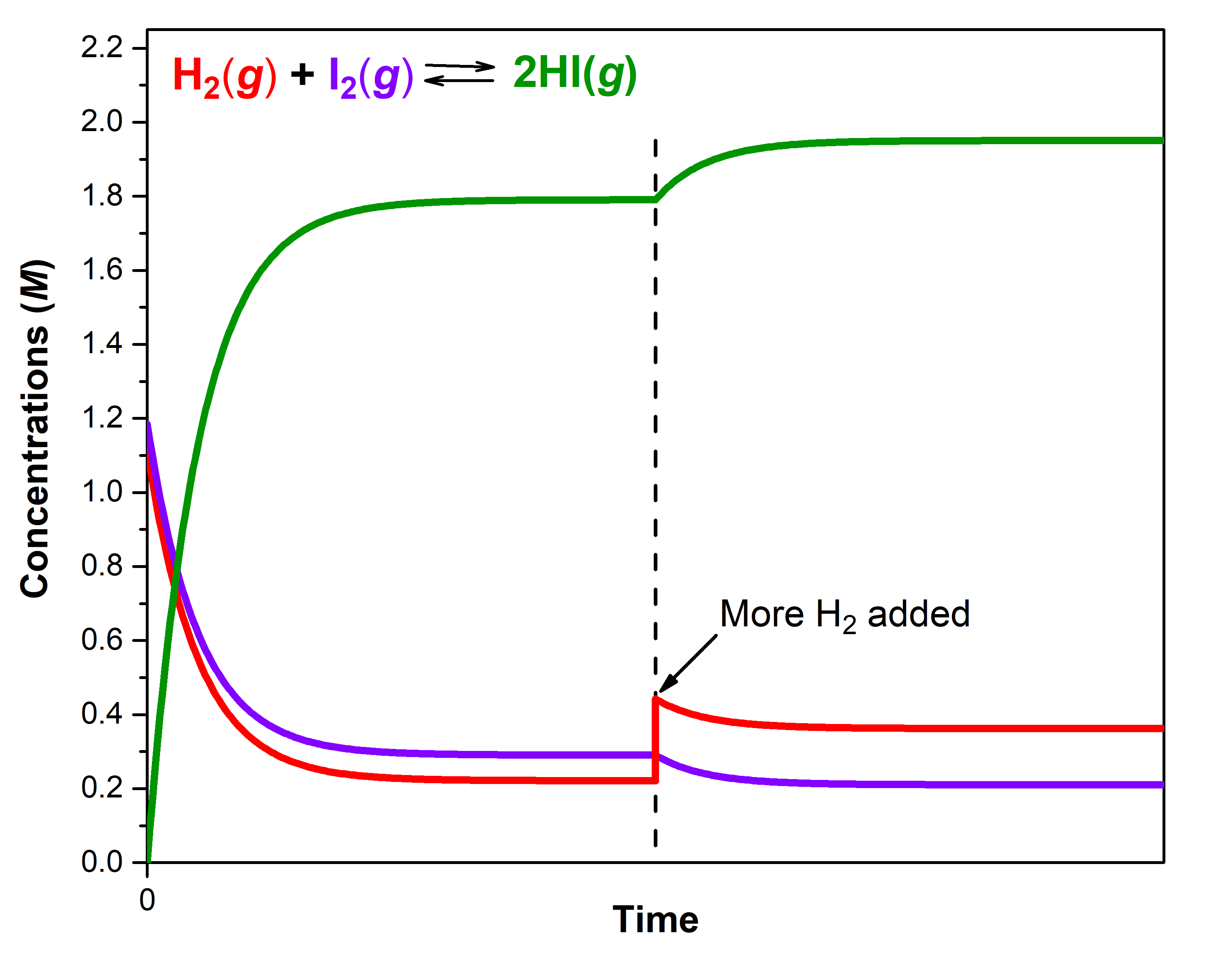
A mixture of gases at 400 °C with [H₂] = 0.221 M, [I₂] = 0.290 M, and [HI] = 1.790 M is at equilibrium in a closed container. For this mixture, Q_c = K_c = 50.0.

If additional H₂(g) is introduced into the container quickly such that [H₂] doubles before it begins to react (that is, the new [H₂]_t = 0.442 M), Q_c is now ½ of K_c:

The reaction will proceed in the forward direction (towards products) to reach a new equilibrium. You can use an ICE table and calculate that the new equilibrium concentrations are [H₂] = 0.362 M, [I₂] = 0.210 M, and [HI] = 1.950 M.

Notice that [H₂]_{new equilibrium} (0.362 M) is less than the doubled concentration (0.442 M) but more than [H₂]_{first equilibrium} (0.221 M). The equilibrium has shifted to partially counteract the change in H₂ concentration. Because of the shift, the concentration of the other reactant decreases and the concentration of the product increases. To verify that these new concentrations are equilibrium concentrations, calculate Q:

The figure below illustrates graphically the effect of adding H₂ to the reaction that was at equilibrium.