D30.3 Kinetic Metastability

At a given temperature, the equilibrium constant and its expression can be used to determine the equilibrium concentrations of products relative to reactants. In other words, chemical thermodynamics describes where the equilibrium lies. However, it does not tell us how fast equilibrium is reached. Chemical kinetics is the study of rates of reactions and provides this vital information. Both kinetics and thermodynamics are needed to characterize a chemical reaction because a useful reaction usually is one where significant quantities of products can be produced in a short time.

When we first considered equilibrium, we utilized a reaction energy diagram to visualize the transformation of cis-1,2-difluoroethene molecules to trans-1,2-difluoroethene molecules.

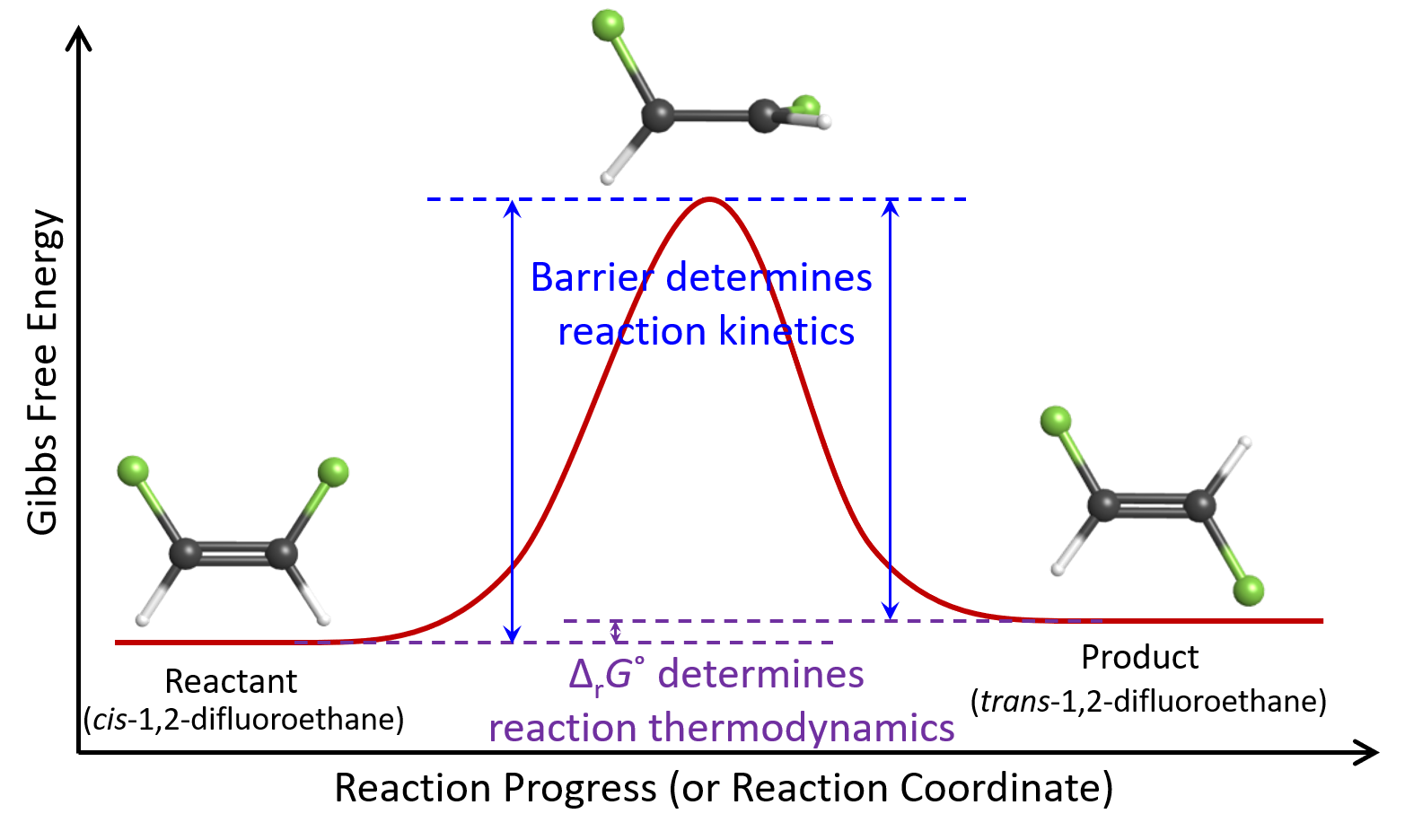
The thermodynamics of this reaction is dictated by the free energy difference (Δ_rG°) between the reactant and the product. The kinetics of this reaction is influenced by the highest energy point in the reaction energy diagram: if a cis-1,2-difluoroethene molecule does not have energy higher than the highest energy point, the reaction will not occur. This “barrier” is the energy needed to rotate around the double bond.

In the upcoming days, we will delve deeper into the study of chemical kinetics. But before we do that, it is useful to distinguish between thermodynamic stability and kinetic metastability. When a reaction favors products at equilibrium (Δ_rG° < 0), we say that the products are thermodynamically stable relative to the reactants. When a product-favored reaction proceeds so slowly that it is considered to not be occurring, we say that the reactant is kinetically metastable (or kinetically stable) relative to product. Note that stability (and metastability) are defined by comparing one substance with another. It is possible that a substance is stable relative to one substance, but unstable relative to another substance.

For an example, consider again the reaction:

Here cis-1,2-difluoroethene has lower Δ_fG° than trans-1,2-difluoroethene, hence Δ_rG° of the forward reaction is positive and reactant is favored at equilibrium. In other words, cis-1,2-difluoroethene is thermodynamically stable relative to trans-1,2-difluoroethene. However, at room temperature, the reaction barrier is high enough that neither forward nor reverse reaction occurs. Therefore, trans-1,2-difluoroethene is kinetically metastable relative to cis-1,2-difluoroethene. We can describe trans-1,2-difluoroethene as being inert (unreactive) at room temperature.

Diamond and graphite are two well-known compounds. They are both composed solely of carbon atoms. The title of an old James Bond film, and an even older advertising slogan, says, “Diamonds Are Forever.” This implies some stability: we don’t expect the diamond in a ring to change anytime soon.

Diamond is kinetically metastable relative to graphite. Thermodynamics says it should change to graphite, but the change is so slow as to be essentially undetectable at day-to-day temperatures in a human lifetime. The fact that diamond exists is due to a very large energetic barrier for conversion of diamond to graphite; diamond would convert to graphite at temperatures of >4500 K.

This very large barrier, as well as the fact that diamond is one of the hardest known solids and graphite is one of the softest, can be explained by differences in the way the atoms are bonded. In diamond, every carbon atom has sp³ hybridization and each sp³ carbon is bonded to 4 other sp³ carbon atoms at the corners of a tetrahedron. In graphite, every carbon atom has sp² hybridization and each sp² carbon is bonded to 3 other sp² carbon atoms in planar sheets of connected benzene rings. Because the sheets can slide past one another relatively easily, graphite is soft and slippery.

Conversion of diamond to graphite requires breaking numerous C−C single bonds with bond energy of 346 kJ/mol. Therefore, transforming diamond into graphite, or vice versa, requires almost as much energy as destroying the entire crystal lattice and rebuilding it. This is why once diamond is formed, it does not convert back to graphite under normal conditions: diamond is said to be metastable because its stability depends on kinetics, not thermodynamics.