D20.7 Molecular View of Equilibrium

The reaction that converts cis-1,2-difluoroethene to trans-1,2-difluoroethene provides a simple example for thinking about equilibrium on the molecular level.

This reaction does not occur at room temperature because it requires breaking the carbon-carbon π bond. But at 615 K (and assisted by a catalyst), 1 mole of cis-1,2-difluoroethene will transform into an equilibrium mixture of ⅔ mole cis isomer and ⅓ mole trans isomer. From a macroscopic point of view, it may appear that the reaction stops once equilibrium is attained, but on the microscopic level, such a statement is untrue.

As cis-1,2-difluoroethene molecules move around in a container at 615 K, energy is constantly being transferred from one molecule to another as they collide. This yields a distribution of kinetic energies, and at any single point in time, a small fraction of cis-1,2-difluoroethene molecules have sufficient energy to convert to the trans isomer. We can think about this pictorially using a reaction energy diagram, which is a diagram that shows energy as a function of reaction progress.

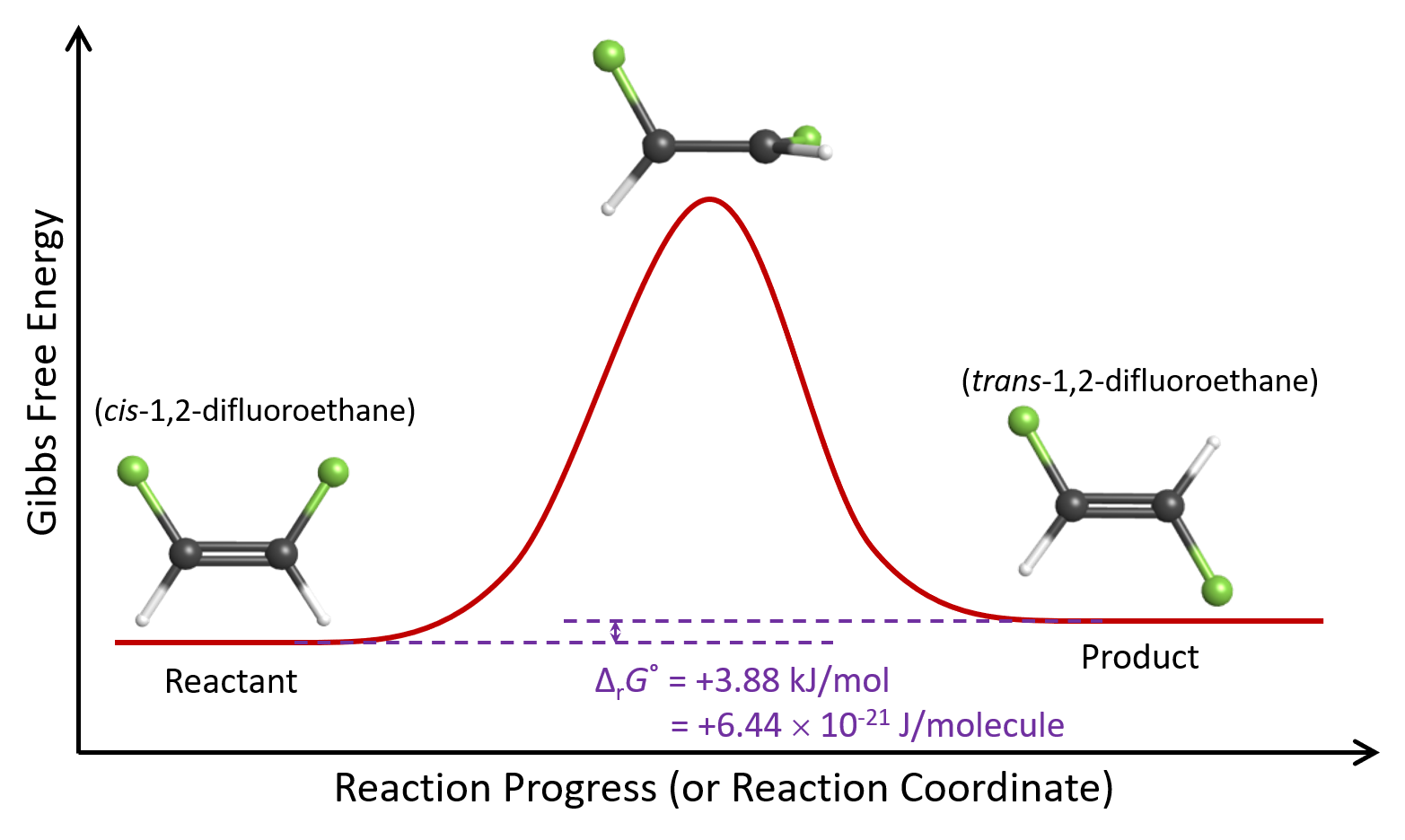
As one end of the molecule rotates relative to the other, energy increases because the π bond is partially broken. When the angle of rotation reaches 90°, the π bond is completely broken. Once the angle exceeds 90°, a new π bond begins to form and the molecule’s energy decreases. Finally, when the angle of rotation is 180°, the new π bond is completely formed and the molecule’s energy has decreased to almost the same value it was initially. (If a molecule does not have energy higher than the highest energy point in the reaction energy diagram, the reaction cannot occur.)

This cis to trans conversion process does not stop when equilibrium has been attained at 615 K. There are still plenty of cis-1,2-difluoroethene molecules present in the equilibrium mixture, and they have the same kinetic energy distribution. Hence, a fraction of them continues to convert to the trans isomer.

If this were the only reaction taking place, the eventual result would be that all the cis isomer would be converted to the trans isomer. This does not happen because the reverse reaction is also occurring at the same time. The trans-1,2-difluoroethene molecules, once formed, also have a distribution of kinetic energies and a fraction of those energies are sufficient for trans-1,2-difluoroethene to convert back into the cis form. Thus cis-1,2-difluoroethene molecules are not only being consumed but are also being produced.

Once equilibrium has been reached, the concentration of cis-1,2-difluoroethene remains constant because the rate at which they are being consumed is exactly balanced by the rate at which they are being produced. In other words, for every cis molecule that converts to the trans isomer, there will be, on average, a molecule of trans isomer converting back to the cis isomer. This constant reshuffle of molecules between reactant (cis-1,2-difluoroethene) and product (trans-1,2-difluoroethene) continues indefinitely without any net change in the concentration of either species.

In this dynamic chemical equilibrium, if you could observe one specific molecule over time, you would find the molecule moving around and often colliding with other molecules. More importantly, sometimes the molecule is in the trans form and other times the molecule is in the cis form.

If we follow this molecule for a while, we would find that, on average, it spends ⅓ of the time in trans form and ⅔ of the time in cis form. This is true for every molecule in the equilibrium mixture. Therefore, at any given moment in time, we find a mixture in which ⅓ of the molecules are trans-1,2-difluoroethene while the other ⅔ are cis-1,2-difluoroethene. The ratio of product to reactant is 1:2, as measured experimentally.

Why is this case? The reason is that the trans isomer is higher in energy than the cis isomer. The change in Gibbs free energy, Δ_rG°, for the reaction is positive:

On average, a molecule spends more time in the lower Gibbs free energy form (cis-1,2-difluoroethene) than the higher free energy form (trans-1,2-difluoroethene).

Looking at the Figure: Reaction Energy Diagram above, we see that it is the Gibbs free energy difference between the reactant and product that dictates their ratio at equilibrium. The highest energy point in the reaction energy diagram dictates how much time it takes to establish equilibrium, a topic that we will discuss in more detail in a later unit.

Let’s consider again the nitrogen dioxide reaction, which involves two reactant molecules:

The sign of Δ_rG° tells us that the product of this reaction is lower in Gibbs free energy than the reactant at 298 K.

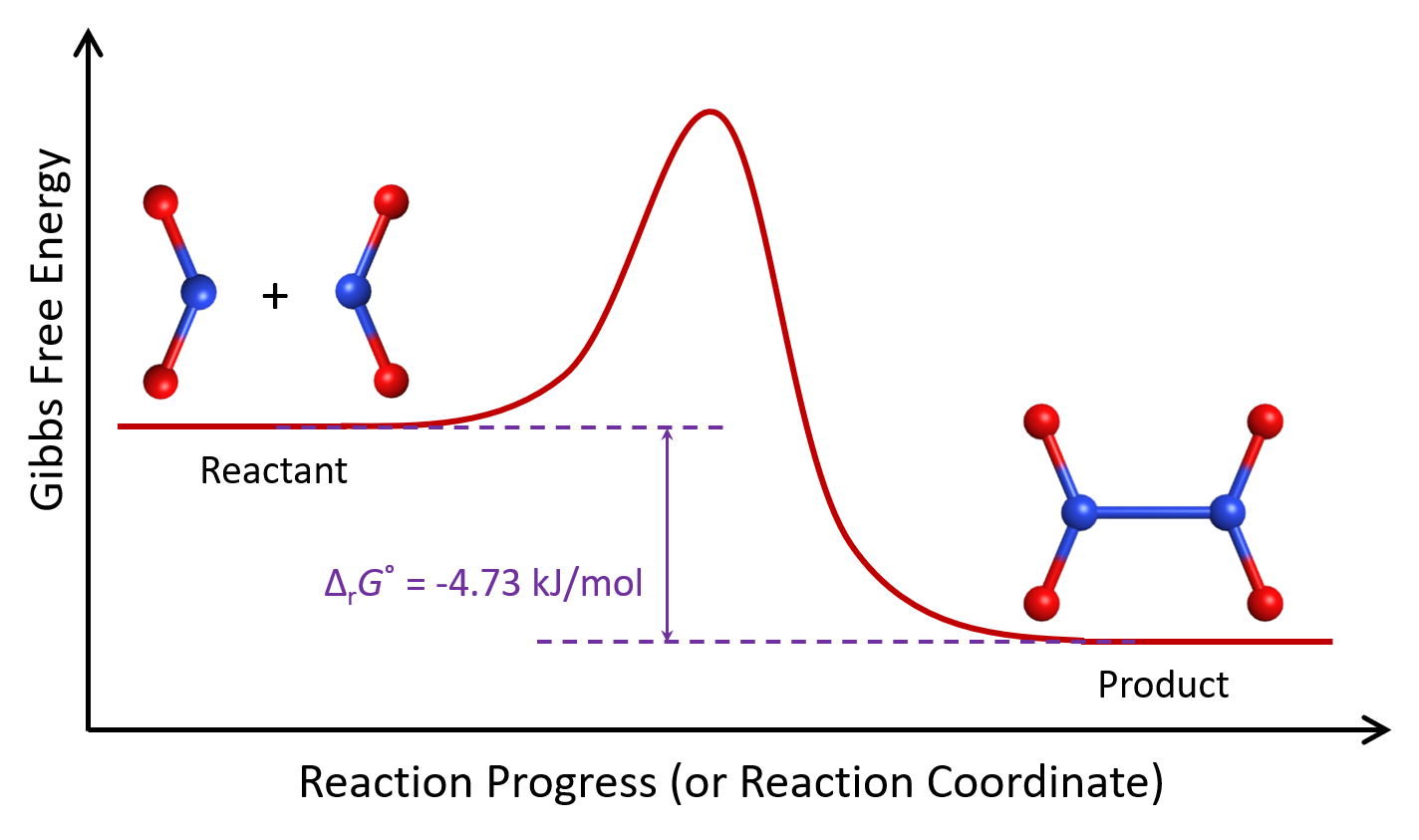
At 298 K, a sizable fraction of NO₂ molecules has sufficient energy to react. If two such NO₂ molecules collide with the N atoms facing each other, allowing for the formation of a N-N bond, a N₂O₄ molecule will form. As the reaction proceeds toward equilibrium, the concentration of NO₂ decreases while the concentration of N₂O₄ increases. A fraction of these newly formed N₂O₄ molecules has sufficient energy for the reverse reaction to occur, thereby producing NO₂ molecules. When equilibrium is reached at 298 K, the reaction vessel contains 70% N₂O₄ and 30% NO₂.

Both the forward and reverse reactions continue to occur after equilibrium has been established. If you could observe one specific NO₂ molecule inside the equilibrium mixture over time, you would see it colliding with many other molecules. A properly oriented collision with another NO₂ molecule could lead to the formation of a N₂O₄ molecule. This N₂O₄ molecule continues to move and collide, and a collision might impart sufficient energy for it to fall apart into two separate NO₂ molecules, one of which is the original NO₂ molecule we were following. If we follow the NO₂ molecule for a while, we would find that, on the average, it spends 70% of the time as a part of a N₂O₄ molecule and 30% of the time as a free NO₂ molecule.

By simply examining this reaction via the Lewis structures of reactant and product, we can see that this reaction has a negative Δ_rH°: a N-N bond is formed and no bonds are broken (both the reactant and product molecules have important resonance structures):

This reaction also has a negative Δ_rS° because two separate gaseous reactant molecules are combining to form a single gaseous product molecule. There is a loss of freedom of motion because a N₂O₄ molecule has to move as a whole while two separate NO₂ molecules can move independently.

Therefore, compared to the cis–trans isomerization example, entropy plays a more important role in this reaction. In the forward direction, this is an exothermic reaction with a decrease in entropy. At temperatures above 52 °C, the magnitude of TΔ_rS° term becomes larger than the magnitude of the Δ_rH° term, and the reaction becomes reactant-favored as the Δ_rG° becomes positive (Gibbs free energy of the product becomes higher than Gibbs free energy of the reactant).

In other words, if the 2 NO₂(g) ⇌ N₂O₄(g) reaction occurred at a higher temperature, for example at 75 °C, the equilibrium mixture would contain more NO₂ molecules (~75%) than N₂O₄ molecules (~25%). On a molecular level, if we follow one NO₂ molecule over time, we would find that as it goes back and forth between being part of a N₂O₄ molecule and being a free NO₂ molecule, it now only spends ~25% of the time as part of a N₂O₄ molecule. Therefore, just like Δ_rG°, the equilibrium state is temperature-dependent. This is true for all processes.

Even though the color stops changing once equilibrium is established at the three different temperatures, both the forward and reverse reactions are still continuously occurring inside each of the three reaction vessels.