D19.4 Entropy and Microstates

An important goal of chemical thermodynamics is to predict whether reactants are changed to products or products are changed to reactants. For a given reaction, such a prediction requires knowledge of specific conditions of temperature and of concentrations or partial pressures of reactants and products. When reactants change to products we say that the reaction is spontaneous, or spontaneous in the forward direction. When products change to reactants, we say the reaction is not spontaneous, or that it is spontaneous in the reverse direction. In this context, the word “spontaneous” does not imply that the reaction is fast or slow, just that reactants change to products. Even if it takes millions of years for a process to occur, if there is an overall change of reactants to products we call the process spontaneous.

It is useful to define parallel terms that relate to a convenient reference point—standard-state conditions. If, when all substances are at the standard-state conditions, reactants change to products, we call a reaction product-favored. In contrast, if products change to reactants under standard-state conditions, a process is reactant-favored. That is, a product-favored process is spontaneous under the specific conditions of standard-state pressures or concentrations and a reactant-favored process is not spontaneous under those specific conditions.

Deciding whether a process is spontaneous requires knowledge of the system’s enthalpy change, but that is not sufficient. It also requires knowledge of change in another property: entropy. (Similarly, deciding whether a process is product-favored requires knowledge of the system’s standard enthalpy change and standard entropy change.) The entropy change, ΔS, at constant temperature is defined as:

{\Delta}S = \dfrac{q_{\text{rev}}}{T}

Here, qrev is the heat transfer of energy for a reversible process, a theoretical process that takes place at such a slow rate that it is always at equilibrium and its direction can be changed (it can be “reversed”) by an infinitesimally small change in some condition. An example of a reversible process is melting water at 0 °C and 1 bar, where liquid water and ice are at equilibrium. Raising the temperature a tiny bit causes the ice to melt; lowering the temperature a tiny bit reverses the process, causing liquid water to freeze.

On a molecular scale, the entropy of a system can be related to the number of possible microstates (W). A microstate is a specific configuration of the energies of a system. The relationship is:

S = kB·ln(W)

where kB is the Boltzmann constant with a value of 1.38×10−23 J/K (or 8.314 J/mol·K).

Similar to enthalpy, the change in entropy for a process is the difference between its final (Sf) and initial (Si) values:

ΔS = Sf – Si = kB·ln(Wf) – kB·ln(Wi) = k_\text{B}\cdot\text{ln}\left(\dfrac{W_{\text{f}}}{W_{\text{i}}}\right)

For processes involving an increase in the number of microstates, Wf > Wi, the entropy of the system increases, ΔS > 0. Conversely, processes that reduce the number of microstates, Wf < Wi, yield a decrease in system entropy, ΔS < 0.

Consider a simplistic case of a system comprised of four distinguishable particles distributed among two energetically-equivalent states, as illustrated in the figure below. The number of microstates possible for such a system is 24 = 16. Microstates with equivalent particle arrangements (not considering individual particle identities) are grouped together and are called distributions. The probability that a system exists as a given distribution is proportional to the number of microstates within the distribution. Because entropy increases logarithmically with the number of microstates, the most probable distribution is the one of greatest entropy.

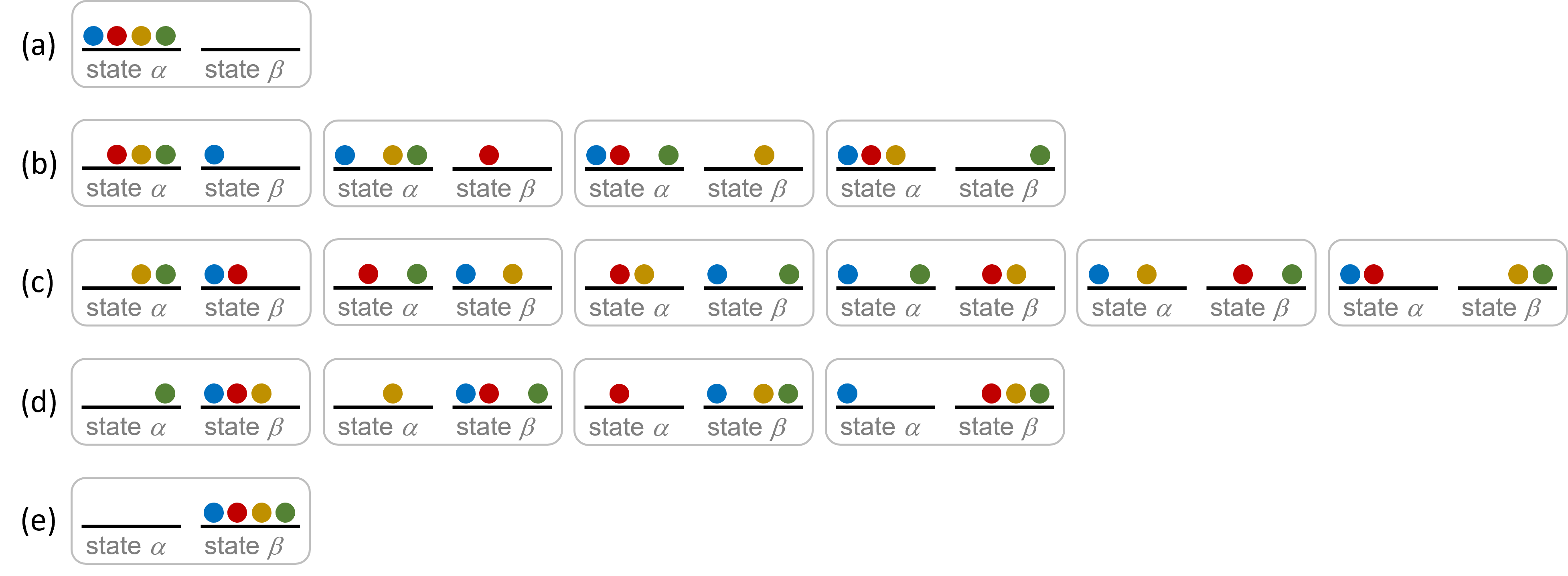
Figure: Microstates. The sixteen microstates associated with placing four distinguishable particles in two states are shown. The microstates are collected into five distributions, (a)-(e), based on the numbers of particles in each of the two states.

For the system in the figure above, the most probable distribution is (c), with the probability of finding the system in this configuration being \frac{6}{16} or 37.5%. The least probable configuration of the system is distributions (a) and (e), where each distribution has a probability of \frac{1}{16} .

Activity: Entropy Change and Microstates

Consider another system as shown in the next figure. This system consists of two objects, AB and CD, and two units of energy (represented as “*”). Distribution (a) shows the three microstates possible for the initial state of the system, where both units of energy are contained within the hot AB object. If one energy unit is transferred, the result is distribution (b) consisting of four microstates. If both energy units are transferred, the result is distribution (c) consisting of three microstates.

Three rows labeled a, b, and c are shown and each contains rectangles with two sides where the left side is labeled, “A,” and “B,” and the right is labeled, “C,” and “D.” Row a has three rectangles where the first has a dot above and below the letter A, the second has a dot above the A and B, and the third which has a dot above and below the letter B. Row b has four rectangles; the first has a dot above A and C, the second has a dot above A and D, the third has a dot above B and C and the fourth has a dot above B and D. Row c has three rectangles; the first has a dot above and below the letter C, the second has a dot above C and D and the third has a dot above and below the letter D.
Figure: Microstate model for heat transfer of energy. This shows a microstate model describing the heat transfer of energy from a hot object to a cold object. (a) Before the heat transfer occurs, the AB object contains both units of energy and the distribution has three microstates. (b) If the heat transfer results in an even dispersal of energy (one energy unit transferred), a distribution of four microstates results. (c) If both energy units are transferred, the resulting distribution has three microstates.

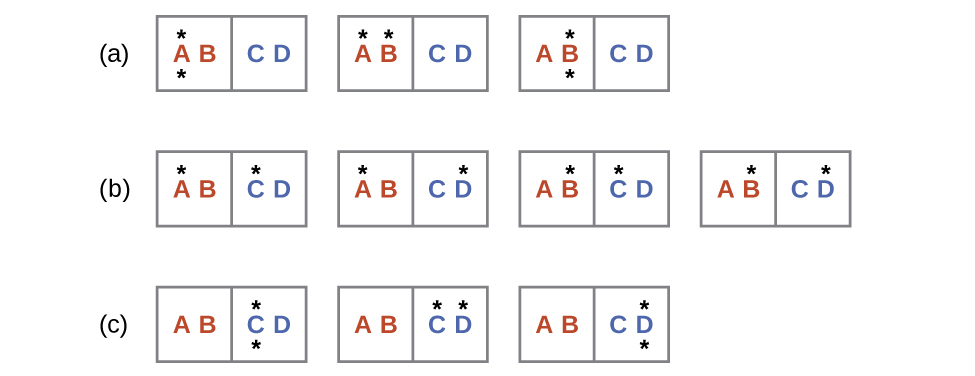
Hence, we may describe this system by a total of ten microstates. The probability that there is no heat transfer of energy when the two objects are brought into contact (the system remains in distribution (a)) is 30%. It is much more likely for heat transfer to occur and yield either distribution (b) or (c), the combined probability being 70%. The most likely result, with 40% probability, is heat transfer to yield the uniform dispersal of energy represented by distribution (b).

This simple example supports the common observation that placing hot and cold objects in contact results in heat transfer that ultimately equalizes the objects’ temperatures. Such a process is characterized by an increase in system entropy.

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry 109 Fall 2021 Copyright © by John Moore; Jia Zhou; and Etienne Garand is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.