D17.4 Enthalpy
Chemical thermodynamics deals with the relationships between heat, work, and other means of energy transfer in the context of chemical and physical processes. Work, represented by w, is a process that transfers kinetic energy to or from a macroscopic object. When a golf club strikes a golf ball, for example, the club does work on the ball, accelerating the ball to a high speed.
Substances act as reservoirs of energy. The total of all possible kinds of energy present in a substance is called the internal energy (U). (The symbol U, instead of E, represents a sum over several different kinds of energy within the substance.) Energy is transferred into a system when it is heated (q) by the surroundings or when the surroundings does work (w) on the system. For example, energy can be transferred into room-temperature metal wire if it is immersed in hot water (the water heats the wire), or if you rapidly bend the wire back and forth (the wire becomes warmer because of the work done on it). Both processes increase the internal energy of the wire, which is reflected in an increase in the wire’s temperature.
The relationship between internal energy, heat, and work can be represented by the equation:
assuming there are no energy transfers other than heat and work. This is one version of the first law of thermodynamics, the law of conservation of energy. The equation shows that the internal energy of a system changes through heat transfer into or out of the system (positive q is heat transfer in; negative q is heat transfer out) or work done on or by the system. The work, w, is positive if it is done on the system (increases the system’s internal energy) and negative if it is done by the system. This is summarized in the figure below.
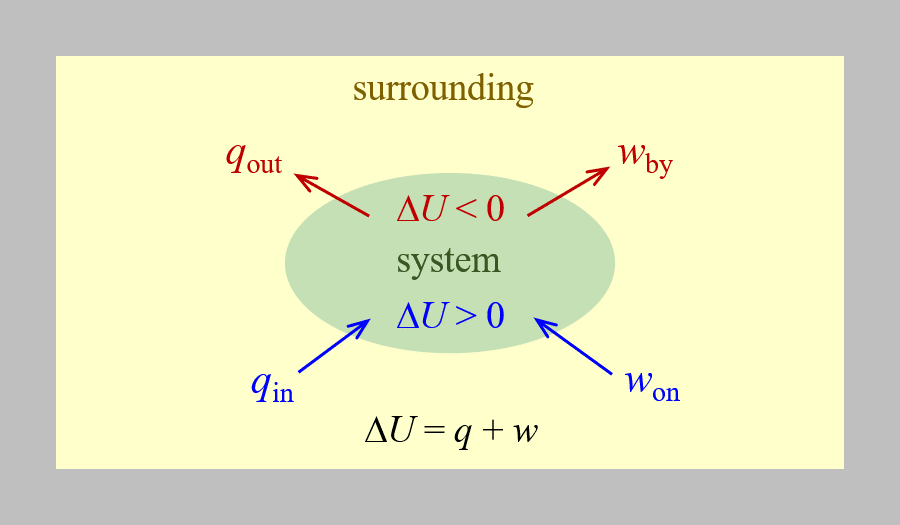
Chemists ordinarily use a property known as enthalpy (H) to describe the thermodynamics of chemical and physical processes.
Enthalpy values for specific substances cannot be measured directly. Only enthalpy changes for chemical or physical processes can be determined. For processes that take place at constant pressure (a common condition for many chemical and physical changes that take place at atmospheric pressure), the enthalpy change (ΔH) for the process is equal to the heat transfer of energy:
The heat transfer to the surroundings when you operate a Bunsen burner is equal to the enthalpy change of the methane combustion reaction that takes place, because the reaction occurs at the essentially constant pressure of the atmosphere. Chemists usually perform experiments under normal atmospheric conditions, at constant external pressure with q = ΔH, which makes ΔH the most convenient choice for determining heat transfer of energy as a result of a chemical reaction.
Consider the process of phase change we explored earlier. On the molecular level, two argon atoms at 377 pm apart require 1.16 kJ/mol to be pulled apart. On the macroscopic level, a sample of liquid argon (for instance, 100 mL of liquid argon) has an enthalpy of vaporization (ΔHvaporization) of 6.4 kJ/mol. This is because each argon atom is surrounded by many other argon atoms in the liquid phase, at various distances apart, and all of those LDFs need to be overcome to bring the argon atoms into the gas phase. Therefore, on average, it takes 6.4 kJ/mol of energy to vaporize a sample of liquid argon.
Enthalpy of vaporization varies with the overall strength of intermolecular interactions. For example, propane (CH3CH2CH3) has ΔHvap = 19.04 kJ/mol, while dimethyl ether (CH3OCH3) has a higher ΔHvap = 21.51 kJ/mol, and ethanol (CH3CH2OH) has an even higher ΔHvap = 38.56 kJ/mol. Therefore, similar to boiling points, we can use enthalpy of vaporization to estimate the strength of intermolecular interactions.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

