Review: Thermochemistry
Heat Capacity
The heat capacity (C) of an object is the heating required to raise an object’s temperature by 1 °C. (Because 1 K is the same size as 1 °C, ΔT has the same numeric value whether expressed in K or °C.) Heat capacity typically has units of J/°C (or J/K). Heat capacity depends on both the type and the quantity of substance, and therefore is an extensive property—its value is proportional to the quantity of the substance.
The specific heat capacity (c) of a substance is the heating required to raise the temperature of 1 g of a substance by 1 °C. It typically has units of J/g·°C. Specific heat capacity depends only on the type of substance and therefore is an intensive property. The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and typically has units of J/mol·°C.
Specific heat capacities of some common substances are listed in the table below.
| Substance | Symbol (state) | Specific Heat Capacity (J/g·°C) |
|---|---|---|
| helium | He(g) | 5.193 |
| water | H2O(l) | 4.184 |
| ethanol | C2H6O(l) | 2.376 |
| ice | H2O(s) | 2.093 (at −10 °C) |
| water vapor | H2O(g) | 1.864 |
| nitrogen | N2(g) | 1.040 |
| oxygen | O2(g) | 0.918 |
| aluminum | Al(s) | 0.897 |
| carbon dioxide | CO2(g) | 0.853 |
| argon | Ar(g) | 0.522 |
| iron | Fe(s) | 0.449 |
| copper | Cu(s) | 0.385 |
| lead | Pb(s) | 0.130 |
| gold | Au(s) | 0.129 |
| silicon | Si(s) | 0.712 |
| Table: Specific Heat Capacities of Common Substances at 25 °C and 1 bar | ||
Exercise: Specific Heat Capacity and Temperature Change
Calorimetry
Calorimetry is an experimental technique used to quantitatively measure heat transfer of energy. Energy is exchanged with a calorimeter, a device with known heat capacity that therefore can relate ΔT to q. A calorimeter must be insulated thermally so that energy does not transfer beyond its physical boundaries. In calorimetry it is useful to define a system, the substance(s) undergoing the chemical or physical change, and the surroundings, everything else that can exchange energy with the system.
For a simple example, consider the situation when we place a piece of hot metal (M) into cool water (W). Here, the heat transfer of energy occurs from metal to water until the two substances reach the same temperature.
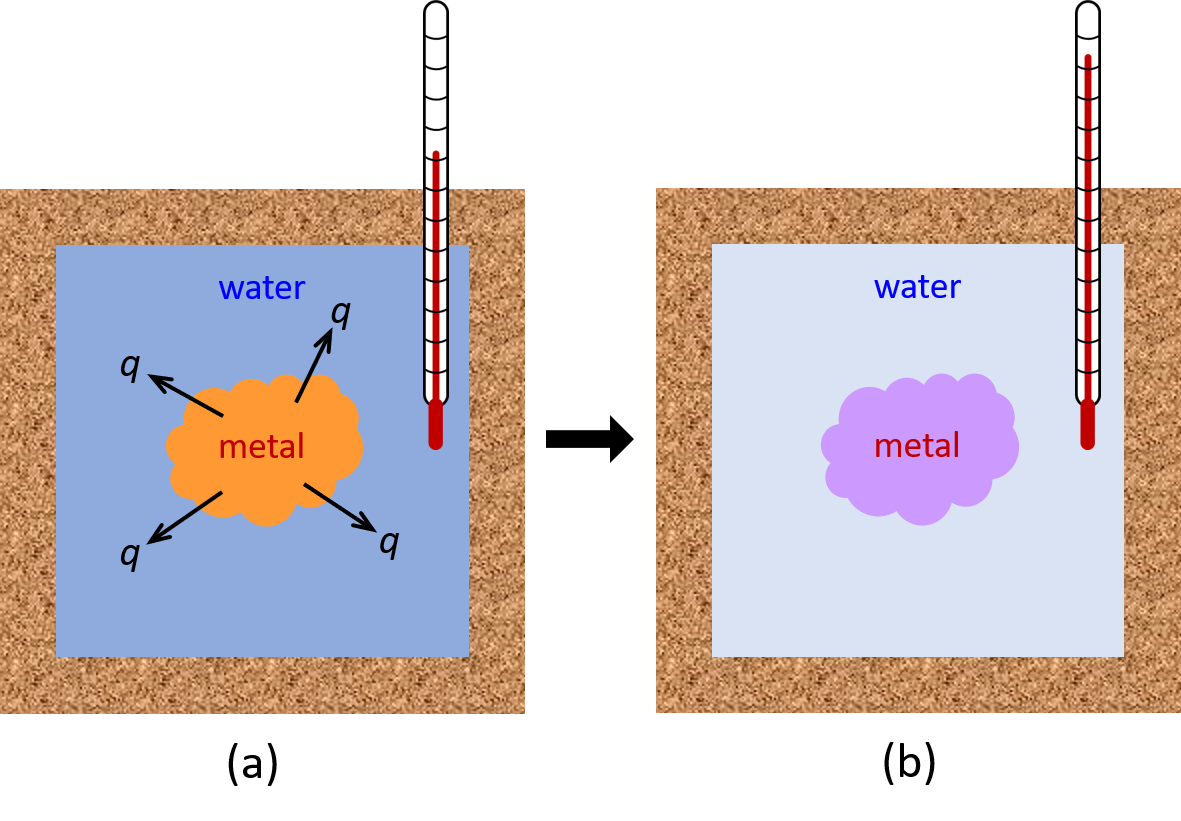
If this occurs in a well insulated calorimeter, this heat transfer would ideally occur only between the two substances. Thus, the magnitude of q is the same for both substances.
The arithmetic sign of q is determined by whether the substance loses or gains energy. In our example, energy is transferred from the metal (qM is negative) to the water (qW is positive).
Exercise: Energy Transfer in a Calorimeter
If the heat capacity of a calorimeter is too large to neglect or if we require more accurate results, then we must take into account energy transferred to or from the calorimeter as well as energy transfers within the the calorimeter. An example of this is a bomb calorimeter, a type of calorimeter that operates at constant volume. Its name stems from it having a strong steel container that will not explode when an exothermic reaction occurs inside it. Bomb calorimetry is used to measure energy transfers for reactions such as combustion reactions. The reaction occurs inside the “bomb” (see the figure below), which is immersed in a water bath and the temperature change of the water bath is measured. Energy has to be transferred to the bomb so the bomb can heat the water, so you need to account for the heat capacity of the bomb as well as the water. That is,

Exercise: Bomb Calorimetry

