D10.5 Types of Hybrid Orbitals
Formation of Hybrid Orbitals
Valence bond theory uses the extent of orbital overlap to infer the strengths of chemical bonds: greater overlap leads to bonds that are stronger and hence a molecule that is more stable. For a given atom in a molecule, overlap with orbitals on other atoms can be greater when some or all of the atom’s valence atomic orbitals (AOs) form hybrid orbitals. Hybrid orbitals are combinations of valence atomic orbitals that emphasize concentration of electron density in specific directions. A hybrid orbital’s greater electron density in a specific direction provides greater overlap with an orbital from another atom when forming a σ bond.
For an example of how orbital hybridization works, consider combining a single 2s AO with a single 2p AO, both on the same atom (Figure below). The 2s AO is spherically symmetric, so it has the same phase (mathematical sign) on either side of the nucleus, but the 2p AO changes sign at the nucleus. Thus, on one side of the nucleus, the 2s and 2p AOs are in phase, while on the other side they are out of phase.
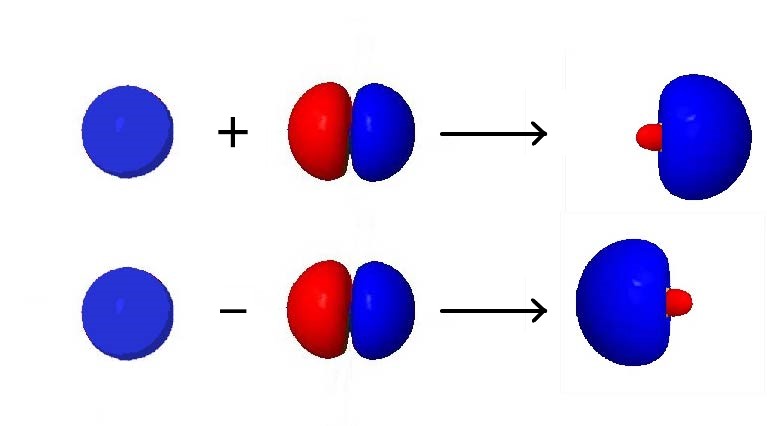
If we add the two AOs, the new hybrid orbital will be larger on the side where the AOs are in phase and smaller on the other side where the AOs are out of phase. If we subtract them, the resultant hybrid orbital will be larger on the side where the AOs are out of phase and smaller where they are in phase. Hence, from one 2s AO and one 2p AO, we can derive two sp hybrid orbitals.
Activity: Orbital Hybridization
sp Hybrid Orbitals
Combining the valence s AO with one of the valence p AOs yields two degenerate sp hybrid orbitals, as shown in Figure: sp Hybrid Orbitals for the case of 2s and 2p AOs. The two sp hybrid orbitals are oriented at 180° to each other—a linear geometry. After the hybridization, there are two unhybridized p AOs left on the atom.
Because these hybrid orbitals are formed from one s AO and one p AO, they have a 1:1 ratio of “s” and “p” characteristics, hence the name “sp”. One of the ways in which the hybrid orbitals exhibit their mixed “s” and “p” characteristics is in their energy. Specifically, the sp hybrid orbitals’ relative energies are about half-way between the s and p AOs from which they are derived, as illustrated in Figure: sp Hybrid Orbitals.
The hybridized orbitals are not energetically favorable for an isolated atom. For example, a beryllium atom is lower in energy with its two valence electrons in the 2s AO than if the electrons were in the two sp hybrid orbitals. However, in a covalent molecule, the one large lobe of each sp hybrid orbital gives greater overlap with another orbital from another atom, yielding lower energy σ bonds.
sp2 Hybrid Orbitals
Combining one valence s AO and two valence p AOs produces three degenerate sp2 hybrid orbitals, as shown in Figure: sp2 Hybrid Orbitals for the case of 2s and 2p AOs. The three sp2 hybrid orbitals are oriented at 120° with respect to each other and are in the same plane—a trigonal planar (or triangular planar) geometry. Each hybrid orbital is pointed towards a different corner of an equilateral triangle. After hybridization, there is one unhybridized p AO left on the atom.
The sp2 hybrid orbitals have twice as much “p” character as “s” character; this is indicated by the superscript “2” in sp2. Energetically, sp2 hybrid orbitals lie closer to the p AO than the s AO, as illustrated in Figure: sp2 Hybrid Orbitals (the sp2 hybrid orbitals are higher in energy than the sp hybrid orbitals).
sp3 Hybridization
Combining one valence s AO and all three valence p AOs produces four degenerate sp3 hybridized orbitals, as shown in Figure: sp3 Hybrid Orbitals (second figure below) for the case of 2s and 2p AOs. The four sp3 hybridized orbitals are oriented at 109.5° with respect to each other, each pointing toward a different corner of a tetrahedron—a tetrahedral geometry.
A tetrahedron is a three-dimensional object that has four equilateral triangular faces and four apexes (corners). All four corners are equivalent. See Figure: Tetrahedron.

An sp3 hybrid orbital has three times as much “p” character as “s” character, hence the superscript “3” in its name. The sp3 hybrid orbitals are higher in energy than the sp2 hybrid orbitals, as illustrated in Figure: sp3 Hybrid Orbitals.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

